Круг знаком вам так же хорошо, как и окружность.
Круг – это часть плоскости, находящаяся внутри окружности, вместе с этой окружностью. Окружность – это граница круга. Центром круга называется центр этой окружности. Радиус, диаметр и хорда круга те же самые, что и у этой окружности. Если в круге провести два его радиуса, например, ОА и ОВ, они выделят из круга его часть, которая называется сектором.

Чтобы вычислить площадь круга удобно разрезать его на секторы, как торт на дольки.
Давайте начертим некоторый круг с радиусом R. И разделим его, например, на 8 секторов. Для наглядности часть секторов заштрихуем.
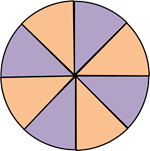
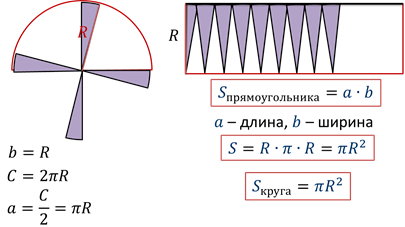
А теперь смотрите, если разрезать круг на секторы, то можно составить новую фигуру.
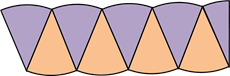
Боковые стороны фигуры можно сделать вертикальными. Для этого давайте крайний левый сектор разрежем пополам и одну из его половинок подставим к правой стороне.
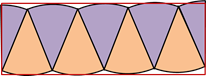
Площадь новой фигуры будет такая же, как и у нашего начального круга. А какую фигуру она вам напоминает? Фигура похожа на прямоугольник!
Если круг разрезать на более мелкие секторы, но новая фигура будет ещё больше похожа на прямоугольник.
Как же вычислить площадь построенной нами фигуры? Мы с вами заметили, что новая фигура очень похожа на прямоугольник. А, следовательно, её площадь можно найти как площадь прямоугольника. Напомним, площадь прямоугольника равна произведению его измерений, или произведению длины и ширины. Ширина получившей фигуры – это радиус нашего круга. Значит, её длина равна R. А как же вычислить длину новой фигуры? Возьмём, к примеру, её верхнюю сторону. Она составлена из дуг половины секторов, на которые мы разрезали круг. Длины же этих дуг в сумме равны половине длине окружности.
Вы уже знаете, что длина окружности вычисляется по
формуле: C = 2πR.
Значит, горизонтальные стороны новой фигуры имеют длину 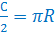 .
А теперь мы можем вычислить площадь новой фигуры. Площадь обозначим буквой S. Тогда получаем,
.
А теперь мы можем вычислить площадь новой фигуры. Площадь обозначим буквой S. Тогда получаем,
Задача
Цирковая арена имеет форму круга. Ее диаметр равен 13,5 м. Вычислите площадь арены цирка (если число π=3,14). Ответ округлите до целых.
Решение:
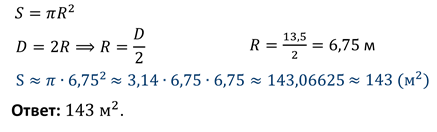
Задача
В Лондоне была построена самая большая в мире
часовая башня, которая имеет название Биг-Бен. Длина окружности циферблата
часов на башне равна 21,98 м. Определите
диаметр и площадь циферблата часов, если число 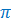 ≈ 3,14. Ответ округлите с
точностью до целых.
≈ 3,14. Ответ округлите с
точностью до целых.
Решение:
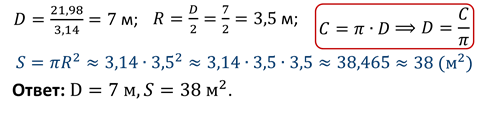

 Получите свидетельство
Получите свидетельство Вход
Вход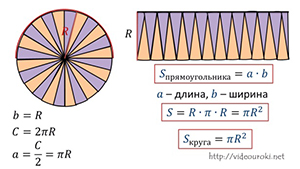



 0
0 3614
3614

