На занятии мы познакомимся с одним интересным семейством линий, одну из которых вы сейчас видите.

Она заключена внутри дракона и своими изгибами обрисовывает его контур. Люди, видевшие драконов, утверждают, что они выглядят именно так.
Давайте возьмём длинную полоску бумаги и пометим её левый конец точкой.

Затем сложим её пополам, чтобы точка оказалась закрытой, а потом ещё раз пополам.


Обратите внимание, что всякий раз мы правый конец накладываем на левый.
Теперь развернём её так, чтобы линии сгибов отчётливо выделялись. Точка должна быть слева. Посмотрите, какая полоска у нас получилась.

Изгибы идут в следующем порядке: вниз – вниз – вверх. А если ввести обозначения (Н – вниз, В – вверх), то это можно записать вот таким образом: Н Н В.
Мы сложили полоску пополам 2 раза. Давайте сложим полоску три раза пополам. Итак, первый раз. Второй раз. И третий раз.




Сейчас развернём её так, чтобы линии сгибов отчётливо выделялись. Получилась вот такая полоска.

В этом случае изгибы идут так: вниз – вниз – вверх – вниз – вниз – вверх – вверх.
Если полоску сложить 4 раза, то изгибы будут идти вот в таком порядке.

А если полоску сложить 5 раз, то изгибы будут идти в следующем порядке.

Эти цепочки букв являются кодами для рисования драконов. Внимательно посмотрим на них и найдём некоторые закономерности.

Итак, в первом случае число изгибов равно 3, во втором – 7, в третьем – 15, а в четвёртом – 31.
Каждый раз получается нечётное число изгибов. Причём, если на
каком-то шаге было  изгибов, то
на следующем их будет
изгибов, то
на следующем их будет  . Проверим
это.
. Проверим
это.
Так как сложив полоску пополам один раз, мы получаем 1 изгиб, то
сложив полоску пополам 2 раза, мы получаем  изгиба.
изгиба.
Сложив полоску пополам 3 раза, мы получаем  изгибов.
изгибов.
Сложив полоску пополам 4 раза, мы получаем  изгибов.
изгибов.
И сложив полоску пополам 5 раз, мы получаем  изгиб.
изгиб.
Обратите внимание, что в каждой цепочке в середине всегда Н. При этом сгибы до этого среднего Н такие же, как и на предыдущем шаге.
И самое главное, что буквы, равноудалённые от среднего Н, всегда различны.
Следуя этим правилам, можно последовательно выписывать цепочки (коды) для полосок, сложенных любое число раз.
Сформулируем общее правило для перехода от одного кода к другому. Берём имеющийся код, приписываем к нему букву Н (под ней удобно поставить точку), затем выписываем в обратном порядке буквы, предшествующие этому Н, заменяя ЭН на В и наоборот.
Пользуясь эти правилом, напишем цепочку-код для полоски, сложенной 6 раз. Для этого возьмём цепочку-код для полоски, сложенной 5 раз. Припишем к нему букву Н (для удобства под ней поставим точку). Теперь будем выписывать в обратном порядке буквы, предшествующие этому Н, заменяя Н на В, В на Н…

Итак, мы научились получать коды сколь угодно длинные.
Как с помощью них построить кривые дракона?
Давайте разберёмся, как следует расшифровывать эти коды для построения кривых дракона. Для этого возьмём лист клетчатой бумаги и проведём в нём вертикальную чёрточку по стороне одной клетки.

Надо заменить в коде букву Н на Л (что означает левый поворот), а
букву В на П (что означает правый поворот). Затем продолжить проведённую
вертикальную чёрточку, следуя командам кода и поворачивая последовательно
налево или направо на  .
.
Очевидно, что, взяв полоску бумаги, сложив её пополам, а затем
развернув, получим один изгиб, который идёт вниз. Н мы заменяем на Л, а значит,
продолжим вертикальную чёрточку, повернув налево на  . Можно
сказать, что получился «дракончик», который соответствует одному складыванию.
. Можно
сказать, что получился «дракончик», который соответствует одному складыванию.

Теперь возьмём код, который получился при двух сгибах полоски. Заменим в нём букву Н на Л, а буку В на П. Получим Л Л П.
Продолжим нашу вертикальную чёрточку, повернув налево на  . Затем ещё
раз повернём налево. Потом повернём направо. У нас получился «дракончик»,
который соответствует двум складываниям.
. Затем ещё
раз повернём налево. Потом повернём направо. У нас получился «дракончик»,
который соответствует двум складываниям.

Возьмём код, который получился при трёх сгибах полоски. Заменим в нём Н на Л, В на П. Получим: Л Л П Л Л П П.
Итак, продолжим вертикальную чёрточку, повернув налево. Снова повернём налево. Затем повернём направо. Опять налево. И ещё раз налево. Потом направо. И снова направо. У нас получился «дракончик», который соответствует трём складываниям полоски.

Построим кривую, которая соответствует четырём складываниям полоски. Возьмём соответствующий код и заменим в нём Н на Л, В на П. Получим: Л Л П Л Л П П Л Л Л П П Л П П.
Продолжим вертикальную чёрточку, повернув налево. Снова повернём налево. Теперь повернём направо. Опять налево. И ещё раз налево. Потом направо. И опять направо. Далее повернём налево. Снова налево. Ещё раз налево. Теперь направо. Опять направо. Затем налево. Снова направо. И ещё раз направо. Получился «дракончик», который соответствует четырём складываниям.

Если внимательно посмотреть на построенные линии, то можно
увидеть, что каждую последующую линию можно получить из предыдущей, добавляя к
ней такую же кривую, но полученную поворотом на  по часовой
стрелке вокруг последней точки.
по часовой
стрелке вокруг последней точки.

Повторение рисунка половины кривой при повороте на  можно
объяснить с помощью исходной бумажной полоски. Возьмём полоску, сложенную
пополам два раза. Очевидно, что в сложенной полоске изгибы слоёв повторяют друг
друга. Развернём эту полоску, чтобы она стала двухслойной. Один слой повернём
вокруг серединного сгиба на
можно
объяснить с помощью исходной бумажной полоски. Возьмём полоску, сложенную
пополам два раза. Очевидно, что в сложенной полоске изгибы слоёв повторяют друг
друга. Развернём эту полоску, чтобы она стала двухслойной. Один слой повернём
вокруг серединного сгиба на  .
.

Получается, что одна половина нашей кривой повернулась на  , повторив
изгибы другой половины.
, повторив
изгибы другой половины.
Таким образом, чтобы построить кривую, соответствующую 5 сгибам
полоски, мы можем взять построенную выше кривую, соответствующую 4 сгибам
полоски. И добавить к ней такую же кривую, но полученную поворотом на  по часовой
стрелке вокруг последней точки.
по часовой
стрелке вокруг последней точки.

Чтобы построить кривую, соответствующую 6 сгибам полоски, мы
возьмём только что построенную кривую, которая соответствует 5 сгибам полоски,
и добавим к ней такую же кривую, но полученную поворотом по часовой стрелке
вокруг последней точки на  .
.

А сейчас давайте полученного дракона нарисуем 4 раза различными цветами. Все они должны «вырастать» из одной точки, но у первого дракона первая чёрточка идёт вверх, у второго – вправо, у третьего – вниз, у четвёртого – влево.
Эти драконы получаются из исходного при помощи трёх
последовательных поворотов на  . При этом
драконы не пересекаются. И последовательно заполняют весь лист бумаги.
. При этом
драконы не пересекаются. И последовательно заполняют весь лист бумаги.
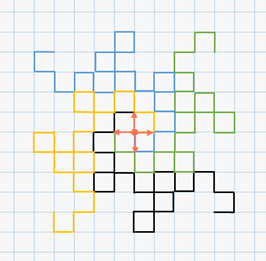
Отметим, что при построении кривых дракона не обязательно всякий
раз поворачивать ранее полученную кривую на  в одном и
том же направлении. Направления вращения (по или против часовой стрелки) можно
чередовать произвольным образом.
в одном и
том же направлении. Направления вращения (по или против часовой стрелки) можно
чередовать произвольным образом.
Так, например, посмотрите на кривую, изображённую на рисунке.

Зелёным кружочком отмечен угол, в котором сделан поворот всей предыдущей кривой против часовой стрелки. Синим кружочком отмечен угол, в котором сделан поворот кривой по часовой стрелке. Из этого дракона можно получить ещё трёх, «растущих» из этой же точки.


 Получите свидетельство
Получите свидетельство Вход
Вход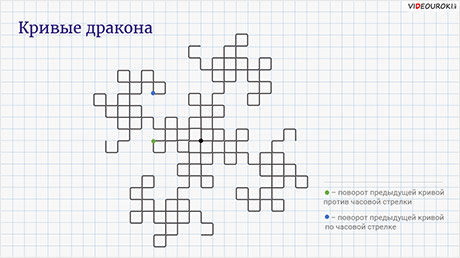




 9108
9108