Ребята, давайте начнём наше занятие с рассмотрения примера.
Согласно СНиП в помещениях, в которых производятся, применяются или хранятся горючие жидкости, полы следует выполнять из негорючих материалов.
Это правило можно сформулировать в виде утверждения: «Если в помещении производятся, применяются или хранятся горючие жидкости, то полы в этом помещении следует выполнять из негорючих материалов». Это сложное утверждение, которое составлено из двух утверждений с помощью слов «если» и «то». Первое утверждение «В помещении производятся, применяются или хранятся горючие жидкости», второе – «Полы в этом помещении следует выполнять из негорючих материалов».
Утверждения, составленные с помощью логической конструкции если …, то …, называют условными утверждениями. Первое утверждение называется условием или посылкой, а второе – следствием.
Рассмотрим следующий пример.
Из курса геометрии известен первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Это только одна из теорем о равенстве треугольников.
Отметим, что в математике каждое утверждение, справедливость которого устанавливается путём рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.
Данная теорема представляет собой условное утверждение. Посылкой является утверждение «Две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника», а следствием – утверждение «Такие треугольники равны».
Также из курса геометрии известна аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Напомним, что аксиома – это высказывание, которое принимается как истинное. Можно сказать, что аксиомы – это фундамент математических рассуждений, начальные истинные высказывания.
Данную аксиому принимают за истинное высказывание. Её можно сформулировать в виде условного утверждения: «Если точка не лежит на данной прямой, то через эту точку можно провести единственную прямую, параллельную данной». Здесь посылкой является утверждение «Точка не лежит на данной прямой», а следствием – утверждение «Через эту точку можно провести единственную прямую, параллельную данной».
Многие математические утверждения – условные. Если такое утверждение удаётся доказать, то получается истинное высказывание. Наиболее важные и общие истинные условные высказывания называются теоремами.
Слова «если» и «то» можно заменить стрелкой. Например, условное утверждение «Из утверждения А следует утверждение В», то есть «Если А, то В», можно кратко записать с помощью стрелки: A → B.
Утверждение A → B ложно, только если посылка А истинна, а следствие В ложно. Во всех остальных случаях утверждение A → B истинно. Таким образом, можно сформулировать следующее правило.
Условное утверждение истинно, если следствие истинно или посылка ложна.
Другими словами, условное утверждение A → B будет ложным только при попытке получить ложь из истины. Во всех остальных случаях утверждение A → B истинно.
Может показаться странным, но истинно даже утверждение «ложь → истина». А всё потому, что из ложного утверждения можно вывести любое следствие – и истинное, и ложное. Иногда говорят: «Из лжи следует что угодно». Точно так же: «Истина следует откуда угодно».
Чтобы понять, истинно или ложно условное утверждение, надо узнать, истинны или ложны его составные части – посылка и следствие.
При установлении истинности условного утверждения удобно пользоваться таблицей.

Рассмотрим ещё один пример. Является истинным или ложным каждое из следующих утверждений?

Конечно же, все эти условные утверждения могут показаться вам странными, но это не мешать определить их истинность.
Первое утверждение ложно, так как в нём из истины следует ложь.
Очевидно, что второе утверждение бессмысленно. Но оно истинно, так как в нём ложная посылка, и из неё можно вывести любое утверждение.
Третье утверждение истинно. А всё потому, что число 11 действительно простое. Посылка здесь тоже истинна, хотя на самом деле это не важно. Достаточно того, что следствие является истинным высказыванием.
А сейчас выполним несколько заданий.
Задание первое. Является истинным или ложным каждое из следующих утверждений?

Решение.
Первое утверждение истинно, так как и посылка, и следствие истинны.
Второе утверждение тоже истинно, так как в нём ложная посылка, а следствие – истинное утверждение.
Третье утверждение ложно, потому что в нём из истины следует ложь.
Четвёртое утверждение истинно, так как в нём ложна посылка и ложно следствие.
Задание второе. К утверждению «Если …, то на этих двух игральных кубиках в сумме выпало 9 очков» подберите посылку так, чтобы оно стало ложным высказыванием.
Решение. Давайте скажем так: «Если на каждом из двух игральных кубиков выпало 3 очка, то на этих двух игральных кубиках в сумме выпало 9 очков».
Мы подобрали посылку таким образом, что это утверждение ложно. Очевидно, что можно подобрать и другие посылки.
Задание третье. К утверждению «Если …, то на этих двух игральных кубиках в сумме выпало 13 очков» подберите посылку так, чтобы оно стало истинным высказыванием.
Решение. Обратите внимание, что следствие в данном утверждении ложно, так как в сумме на двух игральных кубиках может выпасть не больше 12 очков. Тогда чтобы данное утверждение стало истинным, посылка должна быть заведомо ложным высказыванием. Например, на одном из двух игральных кубиков выпало 7 очков.
Получившееся утверждение «Если на одном из двух игральных кубиков выпало 7 очков, то на этих двух игральных кубиках в сумме выпало 13 очков» истинно, так как так как в нём ложна посылка и ложно следствие.
Друзья, на этом мы закончим наше занятие. До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход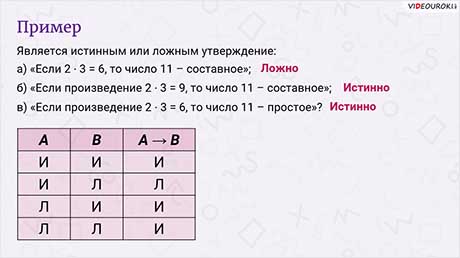




 6017
6017

