Окружность и круг

На этом уроке мы познакомимся с понятиями окружности и круга. Научимся чертить окружность и круг.

Чертить окружности вы научились ещё в младших классах. Давайте вспомним, как происходит этот процесс. Для того чтобы начертить окружность мы должны установить остриё циркуля в некоторой точке О. Далее будем вращать ножку с карандашом.

Определение

Карандаш начертит на плоскости листа линию, которая и называется окружностью. Точка, в которой устанавливалось остриё циркуля, или точка О, называется центром окружности.

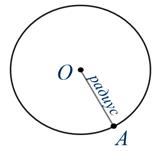
Давайте соединим центр окружности, т.е. точку О, с любой понравившейся вам точкой на окружности. Обозначим эту точку, например, буквой А. Видим, у нас получился отрезок ОА.

Определение

Отрезок, соединяющий центр окружности с любой точкой на окружности, называется радиусом. Радиус обозначают маленькой латинской буквой r.

Отметим на этой окружности ещё несколько точек, например, В, С и D. И соединим их с центром окружности. Эти отрезки ОВ, ОС и OD также называют радиусами.

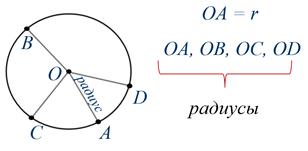
Все точки окружности равноудалены от её центра, т.е. удалены от центра на расстояние, равное длине радиуса.

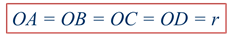
Часто слово «длина» не произносят, а вместо «длина радиуса» говорят просто «радиус». Например, говорят: «Изображена окружность с радиусом, равным 3 см».

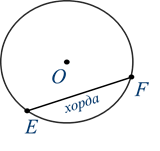
Теперь давайте соединим любые 2 точки на окружности, не проходящие через центр окружности, например, E и F. У нас получился отрезок EF.

Определение

Отрезок, концы которого лежат на окружности, называется хордой.

Хорда, проходящая через центр окружности, называется её диаметром.

Посмотрите внимательно на экран. На рисунке изображён отрезок АВ, он является диаметром окружности. По рисунку нетрудно заметить, что диаметр окружности равен двум её радиусам, т.е.

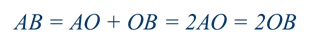
Диаметр обозначают маленькой латинской буквой d, тогда d = 2r.

Запомните, диаметр окружности в два раза длиннее радиуса.

Все диаметры окружности равны между собой.

Отметим на окружности 2 точки, например, M и N.

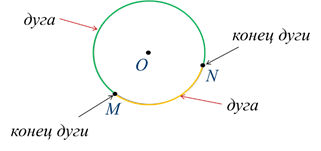
Определение

Эти 2 точки разделили окружность на 2 части, каждую из которых называют дугой.

На нашем рисунке они изображены линиями разного цвета.

Точки M и N называют концами дуг.

Окружность является замкнутой линией. Она разбивает плоскость на две части – внутреннюю и внешнюю.

Часть плоскости, находящаяся внутри окружности, вместе с этой окружностью называется кругом.

Окружность – это граница круга. Центром круга называется центр этой окружности. Радиусом круга называется радиус этой окружности. Диаметром круга называется диаметр этой окружности. Хордой круга называется хорда этой окружности.

Круг состоит из точек, удалённых от данной точки (его центра) на расстояние, меньшее или равное его радиусу.

Определение

Если в круге провести два его радиуса, например, ОА и ОВ, они выделят из круга его часть, которая называется сектором.

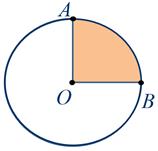
В нашем случае, получился сектор АОВ. Оставшаяся часть круга – также сектор.

Теперь давайте разберёмся с расположением точек, окружности и круга. Посмотрите внимательно на экран.

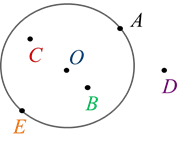
На нём изображена окружность с центром в точке О и точки А, В, С, D и E.

Точки А и Е лежат на окружности или ещё можно сказать принадлежат ей.

Точки В, С, D, O не принадлежат этой окружности.

Точки А, В, С, Е и О принадлежат кругу.

Точка D находится вне окружности или вне круга.

Итоги

Итак, сегодня на уроке мы познакомились с понятиями окружность, круг и их элементами. А также научились их чертить.