Объемы. Объем прямоугольного параллелепипеда

На этом уроке мы узнаем, что такое объём. Научимся находить объём прямоугольного параллелепипеда.

Для начала давайте вернёмся к предыдущим урокам. Мы с вами изучали фигуры, которые расположены в плоскости – это точка, прямая, отрезок, прямоугольник и т.д.. Такие фигуры называют плоскими.

Также мы с вами уже успели познакомиться с прямоугольным параллелепипедом.

Скажите, чем он отличается, например, от прямоугольника? Правильно! Прямоугольный параллелепипед имеет 3 измерения. Такие фигуры как прямоугольный параллелепипед, пирамида, шар и т.д. называют объёмными.

Значит, мы с вами можем найти объём тела. А теперь давайте разберёмся, как же мы будем его вычислять.

Чтобы измерить объём, надо выбрать единицу измерения объёмов.

Определение

Куб, ребро которого равно единице измерения длины, называется единичным.

Объём единичного куба принимается за единицу измерения объёмов.

Например

Точно также определяются и

Легко заметить, что название единицы объёма получается из названия единицы длины присоединением прилагательного «кубический».

Измерить объём тела означает найти число, которое показывает, сколько единичных кубов содержится в этом теле.

Проще всего измерить объём прямоугольного параллелепипеда.

Найдём правило вычисления объёма прямоугольного параллелепипеда.

Пусть у нас есть прямоугольный параллелепипед с измерениями: длина 5 см, ширина 2 см и высота 3 см.

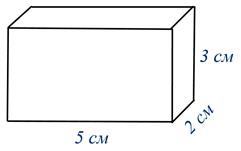
Посчитаем, сколько единичных кубов вмещается в нём. Нижняя грань параллелепипеда имеет длину 5 см и ширину 2 см. Поэтому на ней можно расположить 5 ∙ 2 единичных кубов. Чтобы заполнить весь прямоугольный параллелепипед, нужно вложить 3 таких слоя, т.к. высота параллелепипеда 3 см.

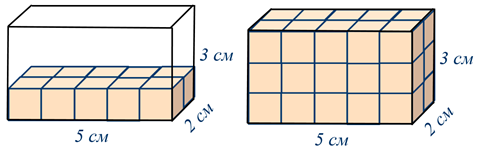
Значит, всего таких кубов, которые вместятся в этом параллелепипеде, будет равно

Запомните, объём прямоугольного параллелепипеда равен произведению трёх его измерений, т.е. длины, ширины и высоты.

Если обозначить объем буквой V, а его измерения: длину – а, ширину – b, высоту – с, то это утверждение можно записать формулой:

При вычислениях нужно обязательно обращать внимание, чтобы все измерения прямоугольного параллелепипеда были выражены в одинаковых единицах.

Если S – площадь основания прямоугольного параллелепипеда, следовательно,

Тогда объём прямоугольного параллелепипеда можно переписать так:

где с – высота параллелепипеда.

Запомните ещё одно утверждение: объём прямоугольного параллелепипеда равен произведению площади основания и высоты.

Найдём правило вычисления объёма куба с ребром а.

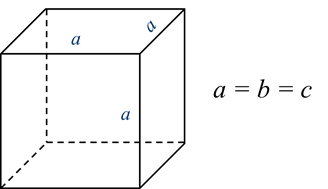
Значит, объём куба можно вычислить так

Именно поэтому  читается «а куб», или «а в кубе».

Равенство V =  даёт возможность выражать одни единицы объёма через другие. Например

Единица объёма 1  имеет ещё и другое название

Итоги

Итак, объём прямоугольного параллелепипеда равен произведению трёх его измерений, т.е. длины, ширины и высоты, V = a ∙ b ∙ c. И ещё объём прямоугольного параллелепипеда равен произведению площади основания и высоты, т.е. V = S ∙ c.