Объем прямой призмы

Сегодня на уроке: мы выведем формулу для вычисления объёма прямой треугольной призмы, произвольной прямой призмы, рассмотрим практическое применение этих формул.

Прежде чем приступить к изучению новой темы, давайте вспомним, что равные тела имеют равные объёмы и если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

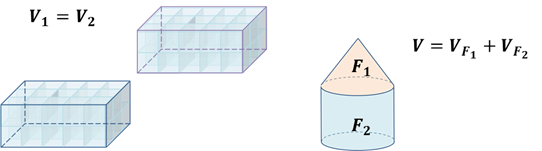
Мы уже знаем, что объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Ещё мы говорили, что:

Объём прямого параллелепипеда равен произведению площади основания на высоту.

Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

Сегодня мы поговорим про объём произвольной прямой призмы.

Давайте сформулируем и докажем теорему: объём прямой призмы равен произведению площади основания на высоту.

Доказательство. Сначала докажем теорему для треугольной прямой призмы.

Рассмотрим прямую треугольную призму  с объёмом  и высотой . Проведём такую высоту треугольника , которая разделяет этот треугольник на два прямоугольных треугольника.

Легко увидеть, что в случае остроугольного треугольника любая высота будет разбивать треугольник на два треугольника. В случае прямоугольного или тупоугольного треугольников, найдется хотя бы одна высота, которая разобьёт треугольник на два треугольника.

Плоскость  разделяет данную призму на две призмы, основаниями которых являются прямоугольные треугольники  и . А мы знаем, что объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

Тогда объёмы  и  соответственно равны:  и .

Тогда общий объём прямой треугольной призмы равен . Вынесем за скобки  и получим в скобках сумму площадей треугольников , то есть площадь треугольника . То есть мы получили, что объём прямой треугольной призмы равен .

Теперь давайте докажем эту теорему для произвольной прямой призмы с высотой  и площадью основания .

Такую призму нетрудно разбить на прямые треугольные призмы с высотой .

Например, пятиугольную прямую призму нетрудно разбить на три треугольные прямые призмы. Как вычислить объём каждой из треугольных призм мы знаем, тогда для того, чтобы получить объём пятиугольной прямой призмы, достаточно сложить объёмы всех треугольных прямых призм . Вынесем общий множитель  за скобки, в скобках получим сумму площадей оснований треугольных призм . А эта сумма есть ничто иное, как площадь основания пятиугольной прямой призмы . То есть получили, что объём прямой пятиугольной призмы тоже равен .

Если прямая призма не пятиугольная, а, например, восьмиугольная, то доказательство проводится аналогично, просто разбивается она не на три, а, например, на шесть треугольных прямых призм.

Таким образом, теорема доказана.

Решим несколько задач.

Задача: найти объём правильной -угольной призмы, у которой каждое ребро равно , если: а) , б) , в) .

Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.

Формулу для вычисления объёма прямой призмы мы только что вывели . Поскольку, по условию все ребра призмы равны , значит, высота призмы равна . Осталось найти площадь основания.

Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник . Площадь правильного треугольника со стороной  вычислить несложно, она равна .

Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен .

Основанием правильной четырёхугольной призмы является квадрат . Площадь квадрата со стороной  равна . Тогда объём правильной четырёхугольной призмы равен .

Основанием правильной шестиугольной призмы является правильный шестиугольник . Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна , значит, площадь правильного шестиугольника равна . Тогда объём правильной шестиугольной призмы равен .

Задача: найти объём прямой призмы  если    и наибольшая из площадей боковых граней равна .

Решение: боковая грань прямой призмы является прямоугольником.

Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.

То есть большая боковая грань содержит большую сторону основания.

По условию  – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона . Вычислим длину стороны  по теореме косинусов.

Получим, что длина стороны .

Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.

Получим, что длина высоты призмы равна .

Для нахождения объёма призмы, воспользуемся только что доказанной формулой . Площадь основания можно найти либо по формуле Герона , либо по формуле .

Мы воспользуемся второй формулой. Получим, что площадь основания равна .

Тогда объём прямой призмы равен .

Задача: наибольшая диагональ правильной шестиугольной призмы равна и составляет с боковым ребром угол в °. Найти объём призмы.

Решение: построим правильную шестиугольную призму и проведём диагональ .

Тогда углом между диагональю и боковым ребром будет угол . Рассмотрим . Поскольку призма правильная, значит,  перпендикулярно основанию, значит,  – прямоугольный треугольник. По свойству катета, лежащего напротив угла в °, . По теореме Пифагора нетрудно найти, что .

Теперь давайте найдём длину стороны основания призмы.

Мы уже говорили, что правильный шестиугольник своими большими диагоналями делится на 6 равносторонних треугольников, тогда одна такая диагональ равна удвоенной стороне шестиугольника. Отсюда получим, что сторона основания равна .

Площадь основания призмы будет равна .

Подставим полученные значения в формулу для вычисления объёма  и получим, что объём правильной шестиугольной призмы равен .

Итоги:

Сегодня на уроке мы вывели формулу для вычисления объёма прямой призмы. В ходе решения задачи вывели формулы для вычисления объёма треугольной правильной призмы, четырёхугольной правильной призмы, шестиугольной правильной призмы, со стороной основания  и высотой . Решили несколько задач с использованием этих формул.