
М - Ох, и устали же мы сегодня. Целый день перетаскивали из угла в угол наш волшебный говорящий буфет.
Помните, как выглядит план наших парадных залов? Мы хотели поставить буфет в один из углов золотого зала. Но, сколько не пытались это сделать, у нас толком ничего не получилось. Если мы приставляли его к одной стене, то между буфетом и другой стеной оставалось пространство. Тогда мы попытались поставить буфет в зелёный зал. Там он вообще не входил ни в один из углов.
- Мы так устали. И теперь просто не представляем, что же нам делать, куда можно поставить наш волшебный буфет.
- Плюс, слышишь, наш компьютер включился. Наверное, сейчас нам по скайпу будет звонить царица Математика.
- Ах, мои дорогие Плюс и Минус! Очень обидно, что прежде чем двигать по всему замку буфет, вы не познакомились с темой «Виды углов». Придётся сегодня мне объяснить вам эту тему.
Итак, сегодня мы поговорим о видах углов - прямых, острых и тупых углах.
- Какие странные названия - прямой, острый, тупой.
- Что же такое угол? Если мы поставим точку, а от этой точки проведём прямую, у нас получится прямая, ограниченная с одной стороны точкой. Такая линия называется луч. А если из этой же точки мы проведём ещё один луч, то у нас получится угол. При этом точка, из которой были проведены лучи, называется вершиной угла, а сами лучи в этом случае называются стороны угла.
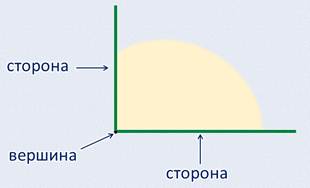
Посмотрите, какие разнообразные углы можно построить:
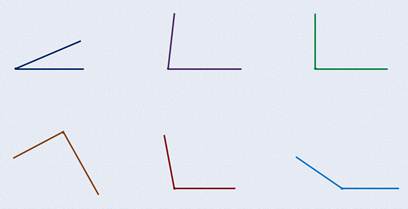
Среди них вы можете увидеть и острые, и прямые, и тупые углы.
- А как же мы отличим, какие из углов острые, какие - прямые, а какие - тупые?
- Начнём мы с прямого угла. Посмотрите на этот лист бумаги. Сейчас мы перегнём его вдвое, потом ещё раз вдвое. Только сгибать надо аккуратно. Так, чтобы линии сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4 раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием листа в четыре раза, называется прямым углом.
А сейчас развернём лист бумаги:
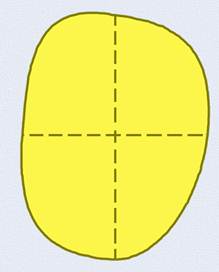
Видите, на нём видны линии сгиба. И у нас видны уже четыре угла с одной общей вершиной. А ещё есть специальная линейка-треугольник. У неё один угол прямой и два острых. Сейчас мы положим такую линейку на наш лист бумаги так, чтобы вершины прямого угла линейки и углов на бумаге совместились. А теперь попытаемся совместить стороны. Получилось?
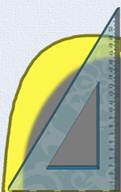
- Да, стороны прямого угла треугольника точно легли на стороны прямого угла на бумаге.
- Теперь так же положим линейку и на остальные три угла. Как видите, и здесь совмещаются стороны. Значит точно, все эти углы одинаковые. Все они – прямые.
- С прямыми углами понятно. А что же это за углы - острые и тупые.
- Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже можно слегка уколоться.
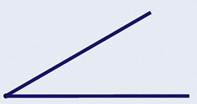
А теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно уколоться. Теперь угол стал тупым:

А теперь давайте вернёмся к тем углам, которые мы нарисовали. Сейчас на первый угол кладём линейку.
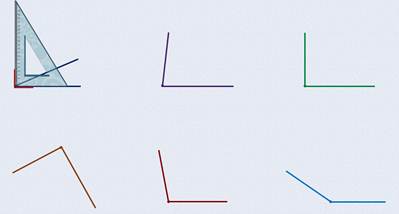
Вершина линейки совмещается с вершиной угла. Одна из сторон линейки совместилась со стороной угла, а вот вторая спряталась под треугольником. Значит, угол раскрыт меньше, чем прямой угол треугольника. Такие углы, которые раскрыты меньше прямого угла, называются острыми углами.
Посмотрите на следующий угол. Он раскрыт значительно шире первого, но, когда мы прикладываем к нему линейку:
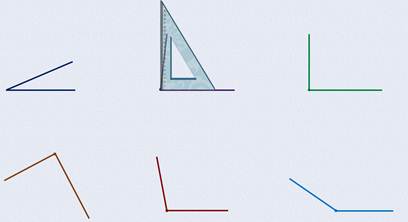
Видно, что одна из сторон опять спряталась под линейку. Значит, этот угол тоже острый.
Переходим к следующему углу:
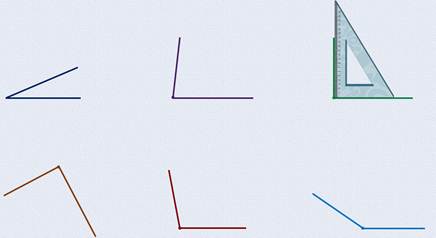
Его вершина и стороны точно совместились с вершиной и сторонами прямого угла линейки. Как вы думаете, какой это угол?
- Конечно, прямой!
- Совершенно верно. Этот угол прямой. А вот этот?
- Наверное, острый. Видите, как он наклонился.
- А если приложить линейку? Ну что, какой угол?

- Я ошибся… Этот угол тоже прямой………….
- Ну что же, продолжим. Рассмотрим следующий угол:

Посмотрите, между второй стороной линейки и стороной нарисованного угла как будто ещё один уголок появился. Значит, этот угол раскрыт немного шире, чем прямой. Такие углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Ну, а если посмотреть на последний угол, то здесь даже без линейки-треугольника понятно, что он тупой.
- Да, это очень хорошо видно. Но мы всё-таки приложим линейку и к нему:
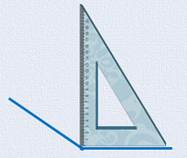
Сейчас очень хорошо видно, что этот угол раскрыт намного шире прямого. Конечно, он - тупой.
Ну что, Плюс и Минус, вы поняли, какие бывают углы?
- Да, поняли. А если присмотреться, то в обычных комнатах все углы - прямые.
- А еще прямые углы у учебников и тетрадей.
- У школьных парт и столов.
- И у нашего волшебного буфета тоже все углы прямые.
- Значит, поставить его можно только туда, где стены образуют прямой угол. Посмотрите ещё раз внимательно на план парадных залов.
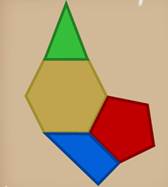
Ну, где вы можете найти прямой угол?
- По-моему, в золотом зале все углы тупые, в зелёном - все острые. А вот прямой….
- Мне кажется, я вижу два прямых угла в синем зале. Но, всё-таки, проверю-ка я это при помощи линейки:
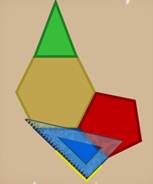
Урра! Получилось! В синем зале- 2 прямых угла. Вот если бы мы сначала поработали с планом парадных залов, не пришлось бы волшебный буфет таскать по всему дворцу.
- Ну, а теперь повторите, пожалуйста, чему вы сегодня научились.
- Угол образуется двумя лучами, которые выходят из одной точки.
- Прямой угол можно получить аккуратным сгибанием листа бумаги вчетверо. Но лучше воспользоваться специальной линейкой-треугольником.
- Углы, которые раскрыты меньше прямого угла, называются острыми углами.
- Углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Хорошо, урок вы усвоили. А теперь за работу - поставьте волшебный буфет туда, куда его можно поставить - в синий зал.
До свидания.
- До свидания, царица. Спасибо за урок!
- До свидания, ребята. Нам пора за работу.

 Получите свидетельство
Получите свидетельство Вход
Вход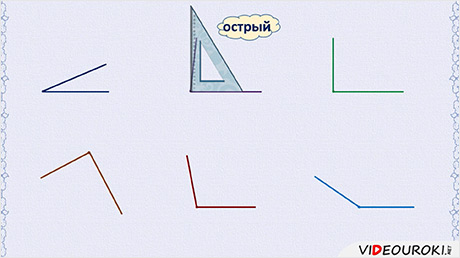



 0
0 11796
11796

