Неравенство треугольника

Вспомним теорему о соотношениях между сторонами и углами треугольника:

В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.

Воспользуемся этой теоремой при доказательстве неравенства треугольника.

Теорема:

Длина любой стороны треугольника меньше суммы двух других его сторон.

Доказательство:

Пусть АВС - произвольный треугольник. Докажем, что сторона АВ меньше суммы сторон АС и ВС.

Отложим на луче АС отрезок СЕ=ВС.

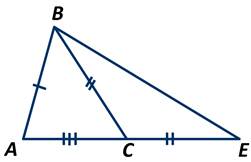
Получили, что треугольник ВСЕ - равнобедренный, а значит, углы при основании равны.

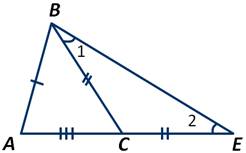
В треугольнике АВЕ угол ∠АВЕ>∠1, следовательно, ∠АВЕ>∠2.

А так как в треугольнике против большего угла лежит большая сторона, то АВ<АЕ.

У нас АЕ=АС+СЕ, а также по построению СЕ=ВС. Тогда получаем, что сторона АВ<АС+ВС.

Теорема доказана.

Следствие:

Для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы следующие неравенства:

Следствие:

Длина каждой стороны треугольника больше разности длин двух других его сторон.

Пример.

Доказать, что медиана АЕ треугольника АВС меньше полусуммы двух соседних его сторон.

Докажем, что для медианы АЕ справедливо неравенство:

Продлим медиану АЕ на её длину, то есть отрезок AЕ=ЕD. Рассмотрим треугольники СЕD и АЕВ.

У них СЕ=ЕВ, так как АЕ - медиана. АЕ=ED по построению, а углы АЕВ и CED равны как вертикальные. А значит, треугольники СЕD и АЕВ равны по первому признаку равенства треугольников. Следовательно, сторона CD=АВ.

В треугольнике CAD по равенству треугольника, получаем:

Что и требовалось доказать.

Пример.

Доказать, что сторона треугольника АВС меньше его полупериметра.

Каждая сторона треугольника меньше суммы двух других его сторон. В нашем треугольнике АВС для стороны АВ имеем:

Прибавим к обеим частям этого неравенства АВ:

Получаем:

Что и требовалось доказать.