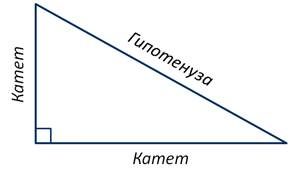
Вспомним, что прямоугольным называют треугольник, который содержит прямой угол. Две стороны, образующие прямой угол, называют катетами, а противолежащую сторону - гипотенузой прямоугольного треугольника.
Теорема:
Сумма углов треугольника равна 180 градусов.
Свойство:
Сумма двух острых углов прямоугольного треугольника равна 90 градусов.
Доказательство:
Пусть АВС - прямоугольный треугольник, у которого ∠С=90 градусов.
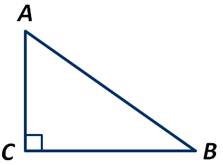
Так как сумма углов треугольника равна 180 градусов, то:
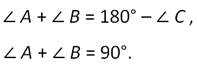
Что и требовалось доказать.
Свойство:
Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.
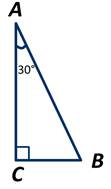
Пусть АВС - прямоугольный треугольник, у которого ∠С=90 градусов, а ∠А=30 градусов. А тогда по теореме о сумме углов треугольника ∠В=60 градусов. Докажем, что катет ВС равен половине гипотенузы АВ.
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:
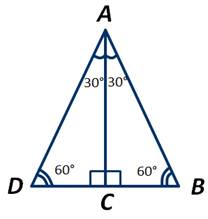
Получили, что у треугольника АВD все углы равны по 60 градусов, то есть он является равносторонним. Получаем:
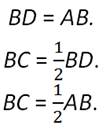
Что и требовалось доказать.
Свойство:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов.
Доказательство:
Пусть АВС - прямоугольный треугольник, у которого катет ВС равен половине гипотенузы АВ. Докажем, что угол ВАС=30 градусов.
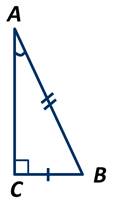
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:
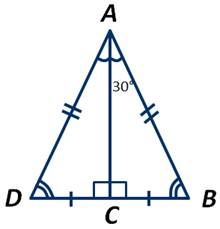
Получили равносторонний треугольник АВD. Известно, что все углы равностороннего треугольника равны 60 градусам. Полуаем:
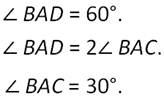
Что и требовалось доказать.
Пример.
Сумма гипотенузы и катета, лежащего против угла в 30 градусов, равна 15 сантиметров. Найти длину гипотенузы.
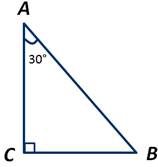
Пусть АВС - прямоугольный треугольник. ∠А=30 градусов. Получим:
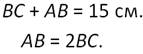
Подставим это в предыдущее равенство и получаем:
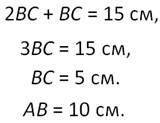
Пример.
В прямоугольном треугольнике АВС, ∠С=90 градусов, а ∠ВАС=60 градусов. Найти длину катета ВС, если высота СD треугольника АСВ равна 5 сантиметров.
Рассмотрим прямоугольный треугольник АВС. ∠АСВ=90 градусов, ∠ВАС=60 градусов. А так как сумма острых углов прямоугольного треугольника равна 90 градусов, то ∠АВС=90-60=30 градусов.
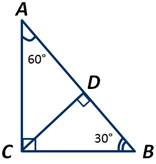
Рассмотрим треугольник ВСD, который является прямоугольным, так как СD - высота и ∠СВD=30 градусов, то катет СD лежит против угла в 30 градусов. Следовательно, по выше доказанному свойству, гипотенуза ВС=2*5=10 см.
Пример.
Отрезок СD - высота прямоугольного треугольника АВС с прямым углом С, ВС=2*ВD. Доказать, что АВ=4*ВD.
Рассмотрим прямоугольный треугольник BCD:
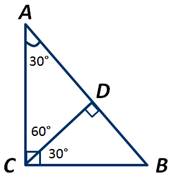
У него ∠ВСD=30 градусов, так как по условию ВС=2*ВD.
По условию задачи ∠АСВ=90 градусов, а ∠ВСD=30 градусов, значит, ∠АСD=60 градусов.
Так как СD - высота, то треугольник АСD - прямоугольный. ∠АСD=60 градусов. Следовательно, ∠САD=30 градусов.
Теперь рассмотрим треугольник АВС. У него ∠ВАС=30 градусов. Следовательно, гипотенуза АВ=2*ВС, так как катет ВС лежит против угла в 30 градусов. По условию задачи ВС=2*ВD.
Получаем, что АВ=4*ВD.

 Получите свидетельство
Получите свидетельство Вход
Вход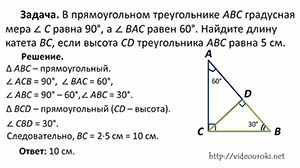



 4
4 89867
89867


замечательно. Спасибо!
-_-
-
+