Признаки равенства прямоугольных треугольников

Первый признак равенства треугольников:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

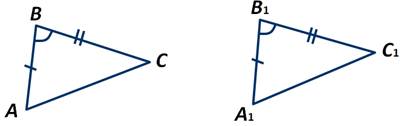
Второй признак равенства треугольников:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

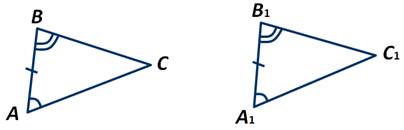
Воспользуемся первым и вторым признаками равенства треугольников и докажем следующие признаки равенства прямоугольных треугольников.

Теорема (о равенстве прямоугольных треугольников по двум катетам):

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

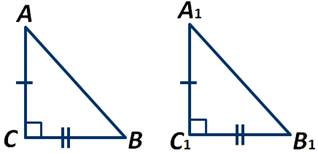
Доказательство:

Возьмём два прямоугольных треугольника АВС и А₁В₁С₁. Пусть катет АС=А₁С₁, а катет ВС=В₁С₁. В прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны. То есть ∠С=С₁=90 градусов. Получаем, что треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников. Теорема доказана.

Теорема (о равенстве прямоугольных треугольников по катету и прилежащему острому углу):

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

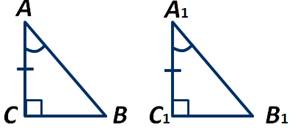
Доказательство:

Пусть АВС и А₁В₁С₁ - прямоугольные треугольники, и катет АС=А₁С₁, а ∠А=∠А₁. А также ∠С=∠С₁=90 градусов. Следовательно, получаем, что треугольники АВС и А₁В₁С₁ равны по второму признаку равенства треугольников. Теорема доказана.

Теорема (о равенстве прямоугольных треугольников по гипотенузе и острому углу):

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

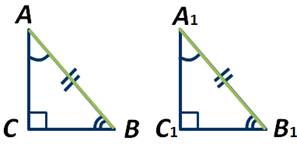
Доказательство:

Пусть АВС и А₁В₁С₁ - прямоугольные треугольники, у которых ∠С=∠С₁=90 градусов. Гипотенузы АВ и А₁В₁ равны. Углы А и А₁ также равны. В прямоугольном треугольнике сумма острых углов равна 90 градусов, то есть:

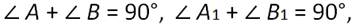
Получаем:

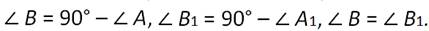
Таким образом, получили, что гипотенуза АВ и два прилежащих к ней угла треугольника АВС соответственно равны гипотенузе А₁В₁ и двум прилежащим к ней углам треугольника А₁В₁С₁. Следовательно, треугольники равны по второму признаку равенства треугольников. Теорема доказана.

Теорема (о равенстве прямоугольных треугольников по гипотенузе и катету):

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольнике равны.

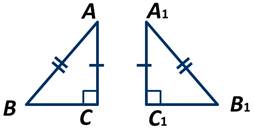
Доказательство:

Пусть АВС и А₁В₁С₁ - прямоугольные треугольники, у которых ∠С=∠С₁=90 градусов. Гипотенуза АВ=А₁В₁ и катет АС=А₁С₁.

Приложим треугольники друг к другу равными катетами, получаем:

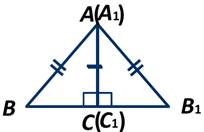
Получили равнобедренный треугольник В₁АВ. АС - высота, проведённая из вершины. Тогда АС является и медианой, то есть В₁С=СВ.

В результате получаем, что у прямоугольных треугольников АВС и А₁В₁С₁ равны и вторые катеты. А следовательно, эти треугольники равны по трём сторонам (или по двум катетам). Теорема доказана.

Пример.

На рисунке отрезки СА и DB перпендикулярны прямой АВ, отрезок ОА=ОВ. Доказать, что отрезок СА=DB.

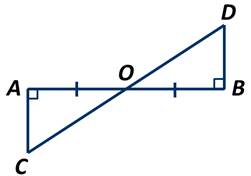
Рассмотрим прямоугольные треугольники АСО и BDO. АО=OB по условию задачи. Углы AOC и BOD равны как вертикальные.

Тогда треугольники АСО и ВDО равны по катету и острому углу. Откуда отрезки СА и DB равны как стороны равных треугольников. Что и требовалось доказать.

Пример.

В треугольниках АВС и А₁В₁С₁ углы С и С1 - прямые, а отрезки АD и A1D1 - биссектрисы. Доказать, что треугольники АВС и А1В1С1 равны, если АD=А₁D₁ и ∠ВАС=∠В₁А₁С₁.

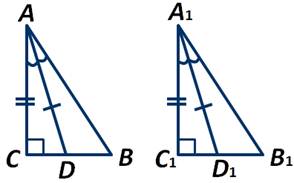
Рассмотрим прямоугольные треугольники АСD и А₁С₁D₁. У них гипотенуза АD=А₁D₁. Углы САD и С₁А₁D₁ равны как половины равных углов САВ и С₁А₁В₁. Получаем, что треугольники АСD и А₁С₁D₁равны по гипотенузе и острому углу. Следовательно, АС и А₁С₁ равны как стороны равных треугольников. Тогда и треугольники АВС и А₁В₁С₁ равны, так как катет АС=А₁С₁ и ∠ВАС=∠В₁А₁С₁. Что и требовалось доказать.