Момент силы. Условия равновесия твердого тела

Данная тема посвящена моменту силы и условиям равновесия твердого тела.

Известно, что основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или же движется равномерно и прямолинейно.

Раздел механики, в котором изучаются условия равновесия материальной точки и абсолютно твердого тела, называется статикой.

Абсолютно твердое тело — это тело, размеры и форму которого можно считать неизменной.

Все опытные факты убеждают в том, что любое тело покоится или движется равномерно и прямолинейно, если равнодействующая всех сил, действующих на него, равна нулю.

Таким образом первое условие равновесия звучит так: векторная сумма приложенных к телу сил должна быть равна нулю.

Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю.

Фактически последние три равенства эквивалентны одному векторному равенству, но с их помощью достаточно просто решать задачи, поскольку проекции сил — это скалярные величины.

В повседневной жизни приходится часто сталкиваться с телами, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и так далее.

Рассмотрим однородное тело в форме диска, которое может свободно вращаться вокруг закрепленной оси, проходящей через его центр.

Если к этому телу приложить силу в некоторой точке А, находящейся под осью вращения, то диск останется в равновесии. Действительно, в этом случае в диске возникнет сила упругости со стороны оси вращения, которая и будет компенсировать воздействие внешней силы.

Если подвесить тело в точке B, находящейся выше или ниже точки «А», то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы можно переносить вдоль линии ее действия. При этом, как видно из рисунка, внешняя сила и сила упругости лежат на одной прямой.

Если же прямая, на которой лежит вектор внешней силы, не проходит через ось вращения, то эта сила не может быть скомпенсирована действием силы упругости оси, и тело начнет поворачивается.

А что произойдет, если к диску приложить не одну, а несколько сил, направленные в разные стороны, например, так, как это показано на рисунке?

Сила F₁ будет стремиться повернуть тело по ходу часовой стрелки, а сила F₂ — против хода часовой стрелки. Так вот, в зависимости от соотношения модулей действующих сил и кратчайших расстояний от оси вращения до линии действия сил, тело повернется в ту или иную сторону.

Если же отношение действующих сил обратно пропорционально этим кратчайшим расстояниям, то тело будет находиться в равновесии.

Данная формула известна из курса физики 7 класса, как условие равновесия рычага.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. А произведение модуля силы на ее плечо называется моментом силы.

Из определения момента силы следует, что единицей его измерения в системе СИ является

Исходя из условия равновесия рычага и определения момента силы, можно сформулировать второе условие равновесия тел. И так, тело находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу, относительно любой оси равна нулю.

Данное условие равновесия является следствием одной из теорем механики — теоремы Вариньона.

Следует напомнить о том, что при использовании правила моментов необходимо учитывать знаки действующих сил. Так обычно считают, что момент силы, которая вызывает вращение тела по ходу часовой стрелки, положителен. И наоборот, если сила пытается повернуть тело против хода часовой стрелки, то момент этой силы считают отрицательным. Однако можно считать и наоборот.

В механике часто возникает необходимость ответить на вопрос: в каких случаях тело может сколь угодно долго оставаться в покое, если оно находилось в покое в начальный момент? Естественно, что должны выполняться условия равновесия. Но практически не во всяком положении равновесия, тело, находящееся в начальный момент в покое, будет оставаться в покое и в последующие моменты времени. Дело в том, что в реальных условиях, помимо учитываемых сил (сила тяжести, сила реакции подвеса или опоры, силы трения и так далее), тело испытывает и не учитываемые случайные воздействия. Это могут быть, например, небольшие сотрясения, колебания воздуха и тому подобное. Под действием таких сил тело хотя бы немного, но будет отклоняться от положения равновесия, а в этом случае дальнейшее поведение тела может быть различным.

Поэтому, для того, чтобы судить о поведении тела в реальных условиях необходимо уметь оценивать равновесие. Различают три вида равновесия — это устойчивое равновесие, неустойчивое равновесие и равновесие безразличное.

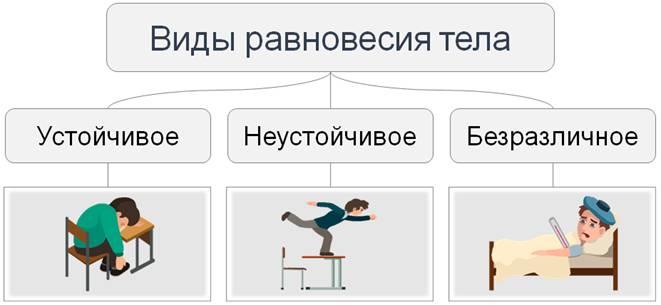
Равновесие тела называют устойчивым, если при отклонении тела от положения равновесия возникают силы, возвращающие тело в положение равновесия.

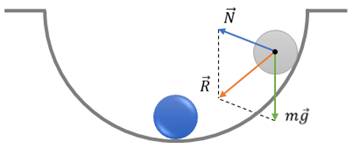
Примером устойчивого равновесия может служить шарик, находящийся на вогнутой поверхности. Если отклонить шарик от положения равновесия, то спустя некоторое временя он вернется в первоначальное положение. Это объясняется тем, что равнодействующая сила в любой точке траектории шарика (за исключением исходной) направлена к положению равновесия.

В устойчивом положении равновесия центр тяжести тела занимает наинизшее из всех близких положений. Тогда очевидно, что такое равновесие тела связано с минимумом его потенциальной энергии.

Если же равнодействующая сила не возвращает тело в первоначальное положение равновесия, а вызывает его дальнейшее отклонение от него, то такое равновесие называется неустойчивым.

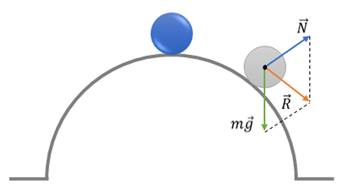
В таком положении, например, находится шарик на выпуклой подставке. При отклонении равнодействующая сила направлена от положения равновесия. В положении неустойчивого равновесия высота центра тяжести тела максимальна. Следовательно, такое равновесие связано с максимумом потенциальной энергии тела.

Если смещения тела в любом направлении не вызывает изменение действующих на него сил (то есть равнодействующая всех сил, приложенных к телу, остается равной нулю), то такое положение равновесия называется безразличным.

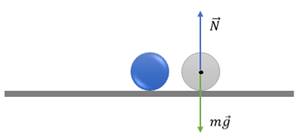
В таком положении находится шарик на горизонтальной плоскости. Безразличное равновесие связано с неизменной потенциальной энергией, а высота центра тяжести тела одинакова во всех достаточно близких положениях.

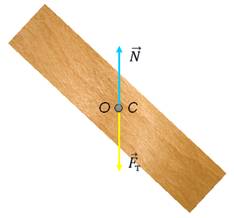
Другим примером равновесий может быть равновесие тела, имеющего ось вращения. В качестве примера рассмотрим однородное тело прямоугольной формы (например, линейку), которое может вращаться вокруг оси, проходящей через точку О.

Линейка будет находиться в устойчивом равновесии, если ее центр тяжести (точка C) находится ниже оси вращения (то есть ниже точки O). При отклонении от положения равновесия возникает момент силы тяжести, который возвращает линейку в положение равновесия. Очевидно, что в отклоненном положении потенциальная энергия линейки больше, чем в положении равновесия. Таким образом, тело, имеющее ось вращения, будет находиться и устойчивом равновесии, если центр тяжести тела находится на вертикальной прямой, проходящей через ось вращения, ниже оси вращения.

Если же центр тяжести находится на вертикальной прямой, проходящей через ось вращения, расположен выше оси вращения, то равновесие будет неустойчивым. В этом случае при отклонении момент силы тяжести отклоняет тело еще дальше от первоначального положения равновесия. При этом потенциальная энергия тела уменьшается.

Если центр тяжести тела и ось вращения будут совпадать, то при любом положении тела момент силы тяжести равен нулю, поскольку равно нулю плечо этой силы. Иными словами, мы с вами будем наблюдать безразличное равновесие. Что касается потенциальной энергии тела, то она будет оставаться неизменной.

Рассмотрим теперь условия устойчивости тела, опирающегося не на одну точку, как в ранее рассмотренных случаях, а на несколько точек (например, стол) или имеющее площадь опоры (например, ящик). В этих случаях для устойчивого равновесия тела необходимо, чтобы вертикаль, проведенная через центр тяжести, проходила внутри площади опоры тела, то есть внутри контура, образованного линиями, соединяющими точки опоры, или внутри площадки, на которую опирается тело.

Если наклонять стол или ящик, то их центр тяжести будет подниматься. Но момент силы тяжести относительно оси вращения будет стремиться вернуть его в первоначальное положение до тех пор, пока линия действия силы тяжести проходит через площадь опоры.

Однако, если их наклонить так, что линия действия силы тяжести выйдет за пределы площади опоры, то тела опрокинутся вследствие действия момента силы тяжести. Очевидно, что имеется предельный угол наклона, то есть угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью, после которого первоначальное равновесие уже не восстанавливается и тело опрокидывается. Этот предельный угол будет тем меньше, чем выше расположен центр тяжести тела при данной площади опоры.

Основные выводы:

Рассмотрены два условия равновесия тел и основные виды равновесия.