Здравствуйте, ребята!

Я хочу вам задать вопрос. Как вы думаете, что общего у колёс велосипеда, вот этих часов и моей любимой пиццы? Догадались? А вот вам ещё загадка.
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
Назовите вы меня!
Ну, теперь вы точно догадались. Конечно, это круг. И сегодня мы с вами поговорим о том, что такое круг и что такое окружность. А еще будем учиться рисовать окружность при помощи циркуля.
В нашей жизни встречается очень много предметов круглой формы. Некоторые из них уже перечислены в загадке. Даже окно в моей комнате — круглой формы. И сейчас каждый из вас вспомнит ещё очень много круглых предметов.
Круглое солнце по небу плывёт,
круг нарисует винтом вертолёт.
Круглая монетка в кошельке лежит,
круглый глазок светофора горит
по круглой арене собачка бежит.
Но прежде, чем получится круг, надо нарисовать окружность. Ну-ка, я попробую нарисовать её.

Да, что-то не очень круглой она у меня получилась. Видимо, надо звать на помощь специальный инструмент для черчения окружностей – циркуль. Вы обратили внимание на то, какое необычное у него имя. Своё название циркуль получил от латинского слова circulus, что в переводе означает круг или окружность.
А вот и он. Вот он встал на свою острую ножку, а второй ногой с закрепленным грифелем обводит… нет-нет, не круг, а именно окружность.
У круга есть одна подруга,
Знакома всем ее наружность!
Она идет по краю круга
И называется – окружность.
А знаете, как-то мой знакомый мальчик Коля Лентяйкин решил нарисовать окружность. Взял циркуль, но получилось у него вот так.

Разве это похоже на окружность? Всё дело в том, что он не закрепил ножки циркуля, и пока он чертил окружность, ножки разъехались. Да еще иголочка циркуля была плохо закреплена, и ёрзала с одного места на другое. Вот и получилось то, что получилось.
Ребята, для того, чтобы окружность получилась ровной и правильной, а не такой как у Коли Лентяйкина, иголочка циркуля должна находиться в одной точке, и ножки должны быть постоянно на одном и том же расстоянии друг от друга. Ну вот, циркуль нарисовал замкнутую кривую линию. А от иголочки остался след-вмятинка, точка. Обозначим её буквой О. И, так как ножки циркуля не разъезжались, а постоянно находились на одном и том же расстоянии друг от друга, значит расстояние от точки О до любой точки, которую можно поставить на линии окружности будет одинаковым. Это можно проверить с помощью линейки. Ставим на окружности несколько точек. Назовём их латинскими буквами К, L, М, N. Теперь измеряем расстояние от точки О до каждой из них. Убедились, что оно одинаковое? Вот поэтому точку О мы называем центром окружности.
Постарайтесь запомнить:
Окружность – это замкнутая кривая линия с центром, который обозначен точкой О. Расстояния от центра до линии окружности одинаковые.
А теперь проведём отрезки от точки О к поставленным на окружности точкам. Полученные отрезки, называются радиусами. Так как расстояния от центра О до любой точки на окружности между собой равны, значит, и радиусы одной окружности тоже между собой равны.
Постарайтесь запомнить:
Радиус – это отрезок, соединяющий центр окружности с любой точкой, лежащей на этой окружности. Радиусы одной окружности между собой равны.
Посмотрите вот на эти два радиуса.
Они встали так, что получился один длинный отрезок, концы которого лежат на окружности, и этот отрезок проходит через центр окружности.
А сейчас я попробую провести еще один такой отрезок – ставлю точку D на окружности и через центр провожу отрезок до другой точки окружности. Назову её точка F.
Когда отрезок проходит через центр, а его концы соединяют две точки окружности, то его называют диаметром.

Если сравнить длину диаметра с длиной радиуса одной окружности, что можно сказать? Так как диаметр образован двумя радиусами, его длина в два раза больше длины радиуса.
Вот я вам всё говорю – окружность, окружность. А вы, наверное, думаете: а что же такое круг? Если окружность — это замкнутая кривая ЛИНИЯ, у которой все точки находятся на равном расстоянии от центра, то круг – это часть плоскости, ограниченная окружностью. То есть окружность – это граница круга.
А теперь давайте вновь вернёмся к диаметру. Как вы думаете, что происходит с кругом, когда мы проводим в нём диаметр? Круг разделился на две равные части. И как бы мы не проводили диаметр – прямо или под наклоном — он всё равно разделит круг пополам, то есть на две равные части.

Ну вот и подходит к концу наша встреча. Я надеюсь, вы смотрели и слушали внимательно, и конечно не забудете:
* Окружность — это замкнутая кривая ЛИНИЯ, у которой все точки находятся на равном расстоянии от центра. Окружность чертят с помощью циркуля.
* Круг – это часть плоскости, ограниченная окружностью. То есть когда мы рисуем окружность, всё, что оказывается внутри неё, и является кругом.
* Радиус – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности. Все радиусы одной окружности между собой равны.
* Диаметр – это отрезок, который соединяет две точки окружности и проходит через её центр. Диаметр делит окружность и круг пополам. Длина диаметра в два раза больше длины радиуса. Все диаметры между собой равны.
А я сегодня прощаюсь с вами. До новых встреч.

 Получите свидетельство
Получите свидетельство Вход
Вход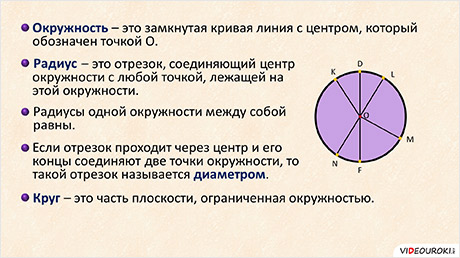




 1941
1941

