Пропорции

На этом уроке мы узнаем, что такое пропорция. Познакомимся с основным свойством пропорции. Научимся решать пропорции. А также ответим на вопрос, является ли данная пропорция верной.

Очень часто в жизни мы сталкиваемся со словом «пропорция». Наверняка вы слышали о пропорциях в человеческом теле!

Вообще пропорция – это широко распространённый термин, который используется во многих областях человеческой деятельности. Можно услышать о пропорциях в кулинарии, медицине, архитектуре.

Также пропорции тесно связаны с наукой. Без пропорций не могут химики, биологи, географы, физики и т.д..

Определение

Само слово пропорция происходит от латинского слова proportio, что переводится как соотношение, соразмерность.

Давайте разберёмся, что же вкладывают математики в слово пропорция.

Рассмотрим два отношения. Мы знаем с прошлых уроков, что отношение – это частное двух неравных нулю чисел (или величин).

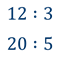
Нетрудно посчитать, чему же равны значения этих частных:

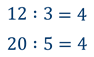
Видно, что и в первом и во втором случае  значения частных равны. А значит и сами отношения равны.

Давайте прочитаем равенство, которое получилось: «12 так относится к трём, как 20 к пяти».

Такое равенство в математике называют пропорцией.

На прошлых уроках мы уточнили, что отношение можно записывать как при помощи знака деления, так и при помощи черты дроби. Следовательно, пропорцию можно записать ещё в виде равенства обыкновенных дробей:

Определение

Пропорция – это равенство двух отношений.

Раз пропорцию можно записать в виде частного двух натуральных чисел, обыкновенными дробями, то пропорцию можно записать и в буквенном виде.

Пропорцию можно прочитать так: «a так относится к b, как c относится к d», или так «отношение a к b равно отношению c к d», или ещё так «a, деленное на b равно c, делённому на d».

Буквенная запись пропорции a : b = c : d – это общий вид пропорции, где: a, b, c и d – называют членами пропорции.

Договариваются, что все члены пропорции отличны от нуля.

a и d – это крайние члены пропорции,

b и c – средние члены пропорции.

Что очень хорошо видно из равенства на экране.

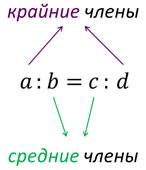
Смотрите a и d расположены по краям пропорции, b и c – посередине. Эти названия сохраняются и тогда, когда пропорция записана в виде:

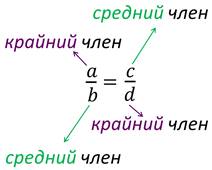
Например

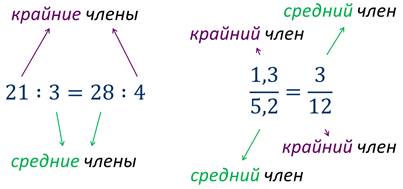
Как вы думаете можно ли как-нибудь убедиться в том, что пропорция составлена верно? Конечно, да!

Рассмотрим пропорцию:

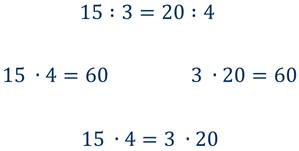
В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции, т.е.

Это утверждение называется основным свойством пропорции.

Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов a · d = b · c, то пропорция a : b = c : d верна. Оно называется признаком пропорции.

Но ведь пропорцию записывают и в виде: 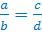. Чтобы не перепутать, какие члены пропорции нужно перемножить, посмотрите, как они расположены в пропорции:

Они лежат «крест-накрест»!

Например, есть пропорция 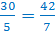. Проверим верна ли она.

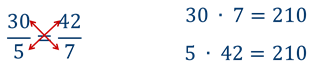
Следовательно, пропорция верна!

Если в верной пропорции поменять местами средние члены и крайние члены, то получившиеся новые пропорции также верны.

Например

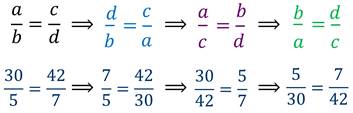
Если три члена пропорции известны, а четвёртый нужно найти, то говорят, что это задача на пропорцию. Задачи на пропорции возникают очень часто. Нужно только научиться уверенно их решать.

Задача

Мама дяди Фёдора из Простоквашино решила сварить для него яблочное варенье из 3 кг яблок. По рецепту на 2 кг яблок нужно 3 кг сахара. Сколько сахара понадобится маме дяди Фёдора для приготовления 3 кг варенья?

Решение:

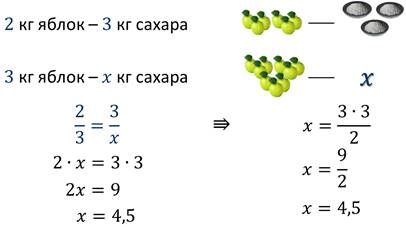
Сформулируем правило для нахождения неизвестного крайнего члена пропорции:

чтобы найти неизвестный крайний член пропорции, нужно произведение её средних членов разделить на известный крайний член пропорции.

Совершенно аналогично формируется правило для нахождения неизвестного среднего члена пропорции:

чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член.

Задание

Найдите неизвестный член пропорции:

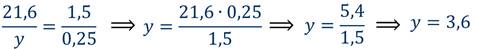
Итоги

Итак, сегодня на уроке мы узнали, что такое пропорция. Познакомились с её основным свойством. Научились решать пропорции. А также, научились отвечать на вопрос, является ли данная пропорция верной.