Отношения

Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.

Для сравнения чисел и величин существуют, как вы знаете, два способа:

1-ый: вычисление разности и 2-ой: вычисление частного.

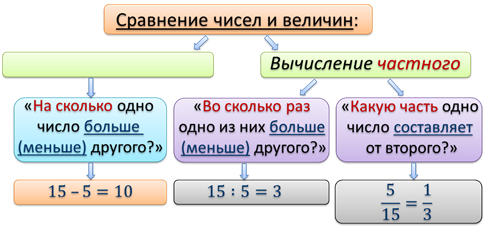
Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.

Задача

На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?

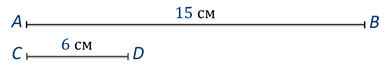
Решение:

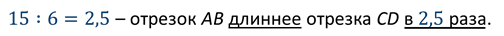
Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?

Решение:

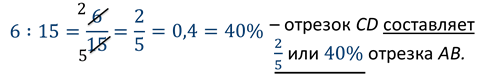
Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением.

Определение

Частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.

Частные чисел читают так:

Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.

Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.

Задача

Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?

Решение:

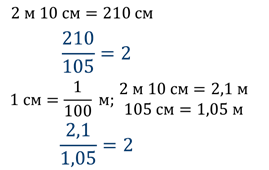
Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.

Итак, если а и b – любые числа, то

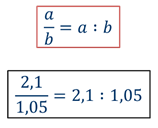
Сделаем важное замечание:

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.

Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.

Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.

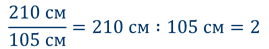
Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.

А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.

Задача

Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.

Решение:

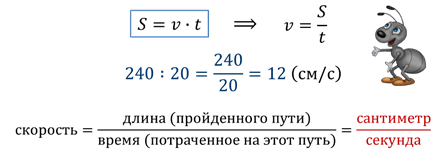
Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.

В виде отношений определяются и другие величины:

Из основного свойства частного следует свойство отношения.

Давайте вспомним основное свойство частного:

если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Следовательно, получаем свойство отношения:

отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Пример

Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.

Итоги       

Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.