Параллелограммы

Проведём две пары параллельных прямых. Образованный при этом четырёхугольник назовём . У этого четырёхугольника сторона  параллельна стороне , а сторона  параллельна стороне . Такой четырёхугольник называется параллелограммом.

Запомните! Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

Посмотрите на следующие фигуры. Каждая из этих фигур является параллелограммом.

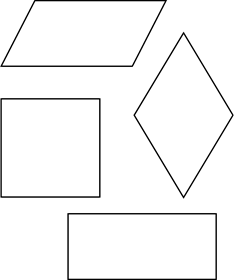
Ромб, прямоугольник и квадрат – тоже параллелограммы. Только это параллелограммы с некоторыми дополнительными свойствами.

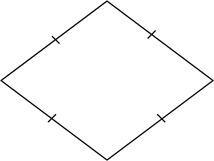
Так, ромб – это параллелограмм, у которого все стороны равны.

А прямоугольник действительно является параллелограммом?

Прямоугольник – это параллелограмм, у которого все углы прямые.

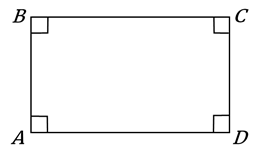
Вспомним свойство, которое говорит о том, что два перпендикуляра к одной прямой, расположенные в одной плоскости, параллельны между собой.

Так как у прямоугольника все углы прямые, то можем записать, что  и . Значит, .

Также запишем, что  и . А значит, .

Получилось, что у прямоугольника стороны попарно параллельны. Следовательно, прямоугольник  является параллелограммом.

А вот квадрат – очень интересный четырёхугольник.

Как и у ромба, у квадрата все стороны равны. Только у него ещё все углы прямые. А значит, квадрат – это ромб, у которого все углы прямые.

Как и у прямоугольника, у квадрата все углы прямые. При этом у него ещё все стороны равны. Значит, квадрат – это прямоугольник, у которого все стороны равны.

Также у квадрата, как и у параллелограмма, стороны попарно параллельны. Только они ещё и равны. Все углы у квадрата прямые. А значит, квадрат – это параллелограмм с прямыми углами, у которого все стороны равны.

Таким образом, из этого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом.

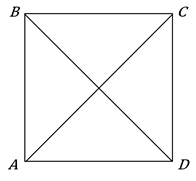
Квадрат обладает рядом интересных свойств. Исследуем с вами квадрат и отыщем его свойства. Но прежде проведём отрезок, который соединяет две противоположные вершины квадрата. Такой отрезок называется диагональю квадрата. У квадрата две диагонали.

Сравним диагонали по длине.

Давайте возьмём квадрат . Проведём диагонали  и . Измерим с помощью линейки длину каждой диагонали. Их длины равны.

Выясним, как диагонали расположены одна относительно другой. Для этого возьмём чертёжный угольник. Совместим точку пересечения диагоналей с вершиной прямого угла угольника и расположим его так, чтобы одна из диагоналей совпала со стороной прямого угла угольника. Видим, что вторая диагональ квадрата совпала со второй стороной прямого угла угольника, а значит, диагонали  и  взаимно перпендикулярны.

Теперь выясним, на какие части делятся диагонали квадрата точкой пересечения. Обозначим пересечение диагоналей квадрата точкой О. Измерим с помощью линейки отрезки  и ,  и . Длины этих отрезков равны: . А значит, диагонали квадрата точкой пересечения делятся пополам.

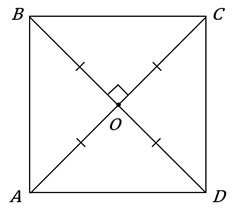
Сформулируем основные свойства квадрата. Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны и точкой пересечения делятся пополам.

Сейчас проведём эксперимент. Возьмём лист бумаги в форме квадрата. Проведём диагональ. Она разделила квадрат на два треугольника. Эти треугольники равны.

Проверим это. Перегнём лист бумаги по диагонали. Видим, что треугольники, на которые диагональ делит квадрат, совпали при наложении, а значит, они равны.

Таким же образом можно проверить равенство треугольников, на которые делит квадрат его вторая диагональ.

Итак, сформулируем ещё одно свойство: диагональ квадрата делит его на два равных треугольника.

А сейчас давайте посмотрим на изображение храма Парфенон в Афинах.

Даже сейчас, когда он стоит в развалинах, – это одно из самых знаменитых сооружений в мире. Храм был построен в эпоху расцвета древнегреческой математики. И его красота основана на математических законах.

Если мы опишем около фасада Парфенона прямоугольник, то окажется, что его длина больше ширины примерно в  раза.

Такой прямоугольник называют золотым прямоугольником. Вычислить точное значение нельзя. Греки умели строить золотые прямоугольники, но не умели находить длины их сторон.

Отличительной особенностью такой фигуры является то, что после удаления квадрата оставшаяся часть остаётся золотым прямоугольником. Проверим это. Вырежем из бумаги прямоугольник со сторонами 13 см и 8 см. Его длина больше ширины примерно в  раза. Убедитесь в этом самостоятельно.

Отрежем от этого прямоугольника квадрат со стороной 8 см. Тогда у нас останется прямоугольник со сторонами 5 см и 8 см. У него также одна сторона больше другой в  раза. Затем от этого прямоугольника отрежем квадрат со стороной 5 см. Останется прямоугольник со сторонами 5 см и 3 см. У этого прямоугольника снова одна сторона больше другой примерно в  раза.

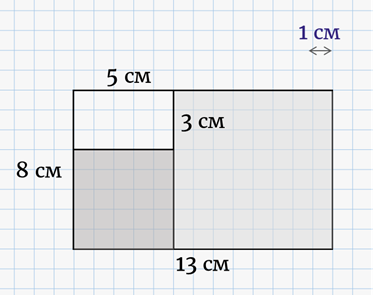
Этот процесс можно продолжать и дальше.

На прямоугольники, в которых стороны относятся как  к 1, обратили внимание очень давно.

Говорят, что стороны золотого прямоугольника образуют золотое сечение. Слово «сечение» здесь употреблено в смысле «деление на части».

Математики дают точное определение золотому сечению. Золотое сечение – это такое деление целого на две неравные части, при котором большая часть относится к целому как меньшая к большей. Число  лишь приближённо (с точностью до ) представляет величину золотого сечения.

Если отрезок разделён на две части так, что меньшая часть имеет длину , а большая часть имеет длину , то в случае золотого сечения длина большей части отрезка относится к длине всего отрезка как длина меньшей части отрезка относится к длине большей части отрезка ().

В правильной пятиконечной звезде каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения.

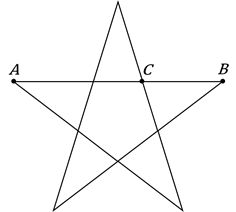
Точка  делит отрезок  на два отрезка –  и .

Тогда

На следующем рисунке изображена раковина. Точка  делит отрезок  приблизительно в отношении золотого сечения.

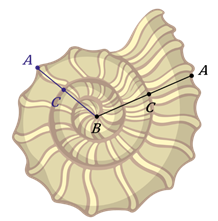
Золотое сечение очень часто использовалось в архитектуре. В природе золотое сечение тоже не редкость. Линия глаз, на которой человек привык концентрировать своё внимание, слушая собеседника, делит длину лица в отношении золотого сечения.

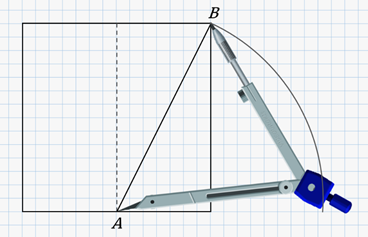
Сейчас давайте с вами построим золотой прямоугольник. Для этого возьмём квадрат и разделим его на два равных прямоугольника. Затем проведём диагональ одного из прямоугольников. Обозначим её. Теперь проведём дугу окружности радиусом  и с центром в точке .

Далее продлим основание квадрата до пересечения с этой дугой. Проведём боковую сторону под прямым углом и закончим построение золотого прямоугольника.