На одном из предыдущих занятий мы с вами рассматривали простейшие
геометрические фигуры, в том числе и углы. И среди всех углов выделили прямой
угол, равный  . Сейчас снова вернёмся к нему. Изобразим прямой угол и продолжим
его стороны за вершину. Мы получили две прямые, которые пересекаются под прямым
углом.
. Сейчас снова вернёмся к нему. Изобразим прямой угол и продолжим
его стороны за вершину. Мы получили две прямые, которые пересекаются под прямым
углом.

Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.
Обозначают перпендикулярные прямые вот так:  ,
,  .
.
Проверить, являются ли прямые перпендикулярными, мы можем, конечно
же, с помощью транспортира. Для этого мы совместим точку пересечения
прямых с серединой транспортира и расположим транспортир так, чтобы одна из его
сторон прошла по линейке. Тогда если вторая прямая проходит через штрих  , то данные прямые пересекаются под прямым углом. А значит, эти
прямые перпендикулярны.
, то данные прямые пересекаются под прямым углом. А значит, эти
прямые перпендикулярны.

Проверить, перпендикулярны прямые или нет, можно также с помощью чертёжного угольника. Для этого нам надо совместить точку пересечения прямых с вершиной прямого угла угольника и расположить его так, чтобы одна из прямых совпала со стороной прямого угла угольника. При этом если вторая прямая совпадёт со второй стороной прямого угла угольника, то значит, прямые пересекаются под прямым углом. Следовательно, данные прямые перпендикулярны.

При этом обратите внимание, что совсем необязательно измерять все четыре угла. Если один угол прямой, то и остальные три тоже будут прямыми.
Строители иногда проверяют перпендикулярность стены основанию дома с помощью отвеса, который представляет собой грузик, подвешенный на тонкой гибкой нити.

Построить перпендикулярные прямые можно с помощью транспортира или чертёжного угольника.
Давайте построим перпендикулярные прямые с помощью транспортира. Проведём
произвольную прямую  . Приложим к этой прямой транспортир так, чтобы она прошла по
линейке. Найдём на шкале штрих, который соответствует
. Приложим к этой прямой транспортир так, чтобы она прошла по
линейке. Найдём на шкале штрих, который соответствует  . И проведём через него прямую
. И проведём через него прямую  , которая и будет перпендикулярна прямой
, которая и будет перпендикулярна прямой  .
.

Теперь построим перпендикулярные прямые с помощью угольника.
Проведём прямую  . Возьмём угольник и совместим сторону его прямого угла с этой
прямой. Затем вдоль второй стороны прямого угла угольника проведём прямую
. Возьмём угольник и совместим сторону его прямого угла с этой
прямой. Затем вдоль второй стороны прямого угла угольника проведём прямую  . Таким образом, мы построили перпендикулярные прямые
. Таким образом, мы построили перпендикулярные прямые  и
и  .
.

Теперь поговорим о свойствах перпендикулярных прямых.
Итак, через точку вне данной прямой можно провести только одну прямую, перпендикулярную этой прямой и пересекающую её.
Так, например, через точку А, которая не лежит на прямой  , можно провести единственную прямую, перпендикулярную данной
прямой
, можно провести единственную прямую, перпендикулярную данной
прямой  . Остальные прямые, проходящие через точку А и пересекающие
прямую
. Остальные прямые, проходящие через точку А и пересекающие
прямую  , являются наклонными прямыми.
, являются наклонными прямыми.

Если точка А будет лежать на прямой  ? В этом случае одна из прямых, проходящих через точку А и
перпендикулярных прямой
? В этом случае одна из прямых, проходящих через точку А и
перпендикулярных прямой  , будет лежать в плоскости тетради, а все остальные (их
бесконечное число) будут прокалывать лист в данной точке. Они будут находиться
вне плоскости листа, то есть в пространстве.
, будет лежать в плоскости тетради, а все остальные (их
бесконечное число) будут прокалывать лист в данной точке. Они будут находиться
вне плоскости листа, то есть в пространстве.

Это напоминает дорожный столб, который стоит на перекрёстке дорог. Он перпендикулярен каждой дороге.

Свойство. Если взять точку на самой прямой, то через эту точку проходит бесконечное число прямых, перпендикулярных данной прямой.
И ещё одно свойство. Две прямые на плоскости, перпендикулярные третьей прямой, не могут пересечься одна с другой.
Пусть прямая  перпендикулярна прямой
перпендикулярна прямой  и пересекает её в точке А. Прямая
и пересекает её в точке А. Прямая  перпендикулярна прямой
перпендикулярна прямой  и пересекает её в точке B. Тогда, если бы прямые
и пересекает её в точке B. Тогда, если бы прямые  и
и  пересеклись, например, в точке C, мы получили бы треугольник ABC, у которого два прямых угла.
А это же невозможно.
пересеклись, например, в точке C, мы получили бы треугольник ABC, у которого два прямых угла.
А это же невозможно.

Поэтому на плоскости такого быть не может. А вот, например, на сфере по-другому. Вспомним экватор и меридианы. Они перпендикулярны друг другу, но при этом все меридианы пересекаются в одной точке – на полюсе.

Поговорим о прямых, которые не пересекаются на плоскости.
Пусть на плоскости дана прямая  и некоторая точка К, которая не лежит на этой прямой.
Проведём через точку К несколько прямых.
и некоторая точка К, которая не лежит на этой прямой.
Проведём через точку К несколько прямых.

Все эти прямые, кроме одной, пересекают прямую  .
.
Назовём эту прямую  . Тогда про прямые
. Тогда про прямые  и
и  мы можем сказать, что они параллельны. Записывают это так:
мы можем сказать, что они параллельны. Записывают это так:  . И говорят: «Прямая
. И говорят: «Прямая  параллельна прямой
параллельна прямой  », или «Прямые
», или «Прямые  и
и  параллельны».
параллельны».
Запомните! Две прямые на плоскости называются параллельными, если они не пересекаются.
Без труда построить параллельные прямые мы можем с помощью чертёжного угольника и линейки.
Давайте проведём прямую, параллельную прямой  , через точку М. Для этого мы совместим сторону прямого
угла угольника с прямой
, через точку М. Для этого мы совместим сторону прямого
угла угольника с прямой  . К другой стороне прямого угла угольника приложим линейку. Теперь
будем двигать наш угольник вдоль линейки до тех пор, пока точка М не
окажется на стороне прямого угла угольника. Затем проведём прямую
. К другой стороне прямого угла угольника приложим линейку. Теперь
будем двигать наш угольник вдоль линейки до тех пор, пока точка М не
окажется на стороне прямого угла угольника. Затем проведём прямую  . Прямые
. Прямые  и
и  параллельны.
параллельны.

Со словом «параллельно» мы иногда сталкиваемся и в жизни. Например, машина может ехать параллельно краю дороги, то есть сохраняя расстояние от края до дороги.
Представление о параллельных прямых мы можем получить, посмотрев на железнодорожные рельсы или на электрические провода.
Так, мы с вами познакомились с перпендикулярными и параллельными прямыми. А также научились их строить с помощью транспортира или угольника. Строить параллельные и перпендикулярные прямые можно также с помощью циркуля и линейки.
Проведём параллельные прямые. Итак, пусть проведена прямая  и отмечена точка А вне этой прямой. Проведём через точку А
произвольную окружность, которая пересекает прямую
и отмечена точка А вне этой прямой. Проведём через точку А
произвольную окружность, которая пересекает прямую  .
.
Одну из точек пересечения окружности с прямой  обозначим буквой B, вторую – обозначим B1. Измерим циркулем отрезок АB и проведём окружность
радиусом, равным отрезку АB, с центром в точке B1. Появится точка A1. Проведём через точки А и A1 прямую
обозначим буквой B, вторую – обозначим B1. Измерим циркулем отрезок АB и проведём окружность
радиусом, равным отрезку АB, с центром в точке B1. Появится точка A1. Проведём через точки А и A1 прямую  . Прямая
. Прямая  параллельна прямой
параллельна прямой  .
.

Теперь проведём перпендикуляр к прямой. Пусть проведена прямая  и дана точка А, которая не лежит на этой прямой. Отметим
на прямой
и дана точка А, которая не лежит на этой прямой. Отметим
на прямой  две произвольные точки. И с помощью циркуля проведём через точку
А две произвольные окружности с центрами в этих точках.
две произвольные точки. И с помощью циркуля проведём через точку
А две произвольные окружности с центрами в этих точках.
Первая точка пересечения этих окружностей – это точка А.
Вторую точку A1. Проведём через эти точки
прямую  . Это и есть перпендикуляр к прямой
. Это и есть перпендикуляр к прямой  .
.

Давайте рассмотрим одно свойство перпендикулярных прямых.
Пусть даны перпендикулярные прямые  и
и  . Если А – точка на прямой
. Если А – точка на прямой  , а B – точка пересечения перпендикулярных
прямых
, а B – точка пересечения перпендикулярных
прямых  и
и  , то отрезок АB есть кратчайшее расстояние от точки А до прямой
, то отрезок АB есть кратчайшее расстояние от точки А до прямой  .
.

Получается, если мы хотим из точки А по кратчайшему пути
попасть на прямую  , то двигаться надо по перпендикуляру к прямой
, то двигаться надо по перпендикуляру к прямой  .
.
Посмотрите на следующие рисунки. На них изображены
перпендикулярные  и
и  ,
,  и
и  . На этих прямых лежат отрезки. Отрезки, лежащие на
перпендикулярных прямых, также называются перпендикулярными. Получается,
что
. На этих прямых лежат отрезки. Отрезки, лежащие на
перпендикулярных прямых, также называются перпендикулярными. Получается,
что  , а
, а  .
.

То же самое мы можем сказать и про отрезки, которые лежат на
параллельных прямых. Отрезки, лежащие на параллельных прямых, также
называются параллельными. Так, например, отрезки  и
и  , которые лежат на параллельных прямых
, которые лежат на параллельных прямых  и
и  , также являются параллельными.
, также являются параллельными.

Теперь посмотрим на куб. Среди его рёбер можно указать пары параллельных и перпендикулярных рёбер.


Через рёбра  и
и  можно провести плоскость
можно провести плоскость  . Эту плоскость называют диагональным сечением куба.
. Эту плоскость называют диагональным сечением куба.
А вот если мы посмотрим на пару рёбер  и
и  . Они не пересекаются, но при этом мы не сможем назвать ни одной
плоскости, которая бы проходила через оба эти отрезка (либо через прямые
. Они не пересекаются, но при этом мы не сможем назвать ни одной
плоскости, которая бы проходила через оба эти отрезка (либо через прямые  и
и  ).
).
Запомните! Прямые, которые не пересекаются, но не лежат в одной плоскости, называются скрещивающимися.

 Получите свидетельство
Получите свидетельство Вход
Вход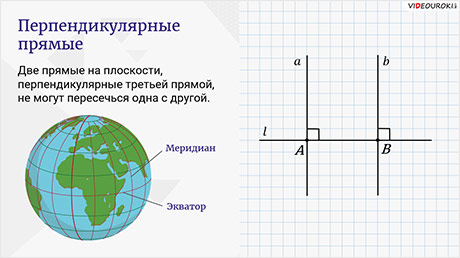




 7979
7979