В данной теме будет рассмотрено решение задач на построение изображений в линзе.
Задача 1. На рисунке изображен предмет АВ и собирающая линза. Постройте изображение предмета если он находится а) за двойным фокусом б) между фокусом и двойным фокусом.
РЕШЕНИЕ
Изобразим на чертеже собирающую линзу, её главную оптическую ось, фокусы и двойные фокусы.

Двойной фокус – это точка, находящаяся на оптической оси на расстоянии от оптического центра, вдвое большем, чем фокусное расстояние. Изобразим предмет АВ, находящийся за двойным фокусом.
Точка А находится на оптической оси линзы, поэтому её изображение тоже будет находится на оптической оси. Чтобы получить изображение точки В, понадобится два луча. Один направим параллельно оптической оси, а второй – через оптический центр. Лучи, проходящие через оптический центр, не преломляются, поэтому легко можем продолжить последний луч. Луч, параллельный оптической оси преломляется, и после преломления проходит через фокус линзы. На пересечении этих лучей и формируется изображение точки В, которое обозначим как B’. Точка A’ будет находится на главной оптической оси.
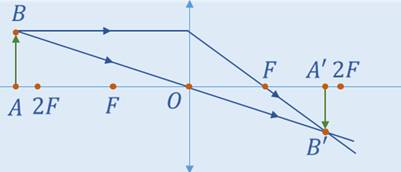
Во втором случаи поступаем таким же образом используя два луча.
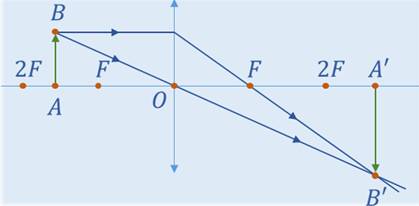
Таким образом, получено действительное и перевёрнутое изображение. Только в этот раз оно является увеличенным и находится за двойным фокусом.
Задача 2. На рисунке указан источник света и его изображение в линзе. Также на рисунке указана главная оптическая ось линзы. На основании этих данных, найдите положение оптического центра линзы, её фокусов, а также определите тип линзы.

РЕШЕНИЕ
В первую очередь, проведём прямую через источник света и его изображение (она называется побочной оптической осью). Точка пересечения этой прямой с главной оптической осью является оптическим центром линзы.
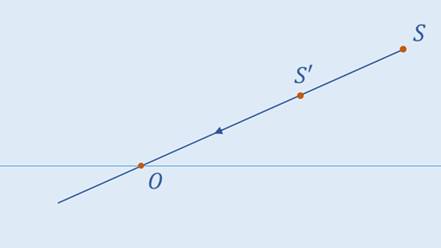
Обозначим на нашем чертеже линзу. От источника света направим луч на линзу параллельно главной оптической оси. Известно, что луч преломляясь идёт через фокус и через изображение (или же, через изображение идёт продолжение луча). Проведём пунктирную прямую через точку, в которой луч падает на линзу и через изображение источника света. Точка, в которой данная прямая пересекает главную оптическую ось и будет являться фокусом линзы.
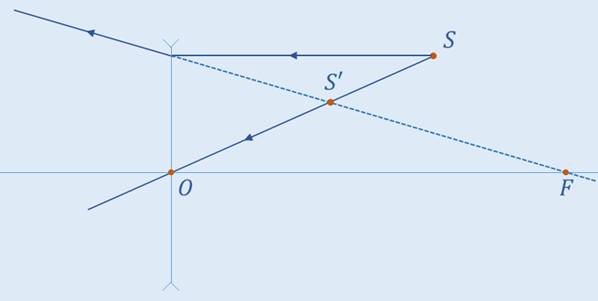
Теперь, с уверенностью можно сказать, что прямая, которую построили является продолжением преломлённого луча. По характеру преломления луча или, исходя из того, что изображение мнимое и находится ближе фокуса, можно заключить, что линза является рассеивающей.
Задача 3. На рисунке изображен луч АВ, прошедший через рассевающую линзу. Также, на рисунке указаны положения фокусов линзы. Постройте ход падающего луча.
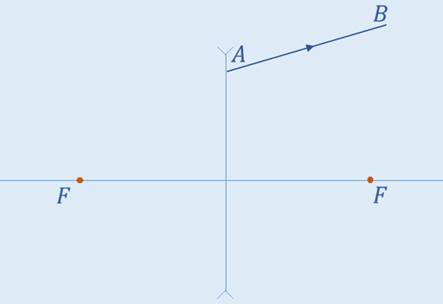
РЕШЕНИЕ
Отметим на чертеже оптический центр линзы. Поскольку имеются положения фокусов линзы, можно провести фокальную плоскость. Теперь проведём продолжение преломлённого луча до пересечения с фокальной плоскостью. Точку пересечения обозначим за F’.
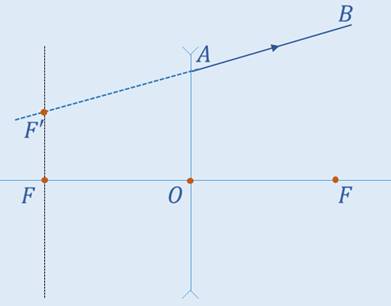
Через эту точку и оптический центр линзы пройдёт побочная оптическая ось. Луч, идущий вдоль этой оси пройдёт, не меняя своего направления (поскольку он пройдёт через оптический центр). Луч, параллельный побочной оси, преломляется таким образом, что продолжение преломлённого луча пройдёт через точку F’. Таким образом, построен падающий луч.
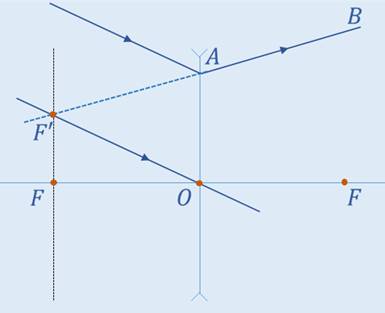
Задача 4. Постройте изображение предмета АВ в соответствии с указанным рисунком.
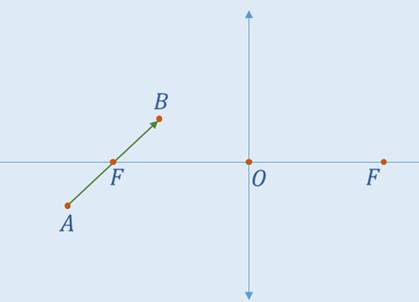
РЕШЕНИЕ
Здесь сложность заключается в том, что предмет проходит через фокус, причём, таким образом, что часть предмета находится на расстоянии, ближе фокусного, а часть – между фокусом и двойным фокусом.
Можно попытаться разбить предмет на два отрезка: AF и FB. Очевидно, что изображения и того, и другого отрезка будут уходить в бесконечность, поскольку, точка F, естественно, находится на фокусном расстоянии от линзы. А, как изветно, изображения предметов, находящихся на фокусном расстоянии от линзы, не формируются (или формируются в бесконечности).
Однако, следует заметить, что луч, идущий в направлении от точки А к точке В преломляется таким образом, что преломлённый луч параллелен главной оптической оси. Можно построить продолжение этого луча.
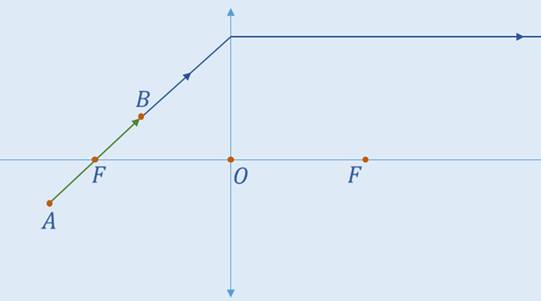
Таким образом, все точки изображения предмета АВ будут лежать на прямой, проходящей через указанный луч и его продолжение. Проведём прямую через точку А и оптический центр до пересечения с указанной ранее прямой. В точке пересечения получится изображение точки А, которое обозначим как A’.
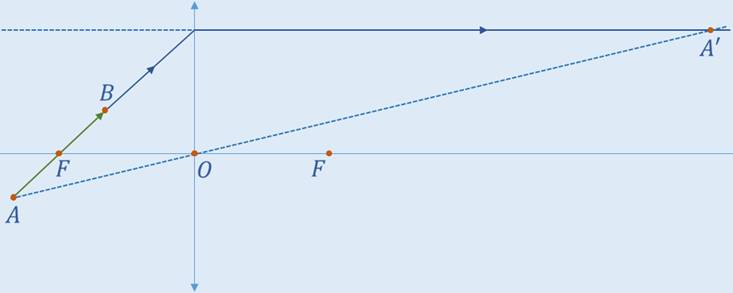
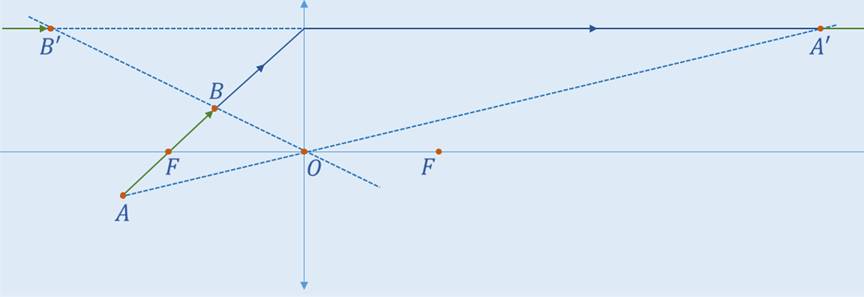
Аналогично, проведём прямую через оптический центр и точку D – таким образом, получим точку B’. Если попытаться получить изображения других точек аналогичным способом, то можно убедиться, что изображение данного предмета получается разрозненным (то есть, делится на две части). Действительно, ведь изображение той части предмета, которая находится перед фокусом, является мнимым, а изображение части, находящейся между фокусом и двойным фокусом является действительным.
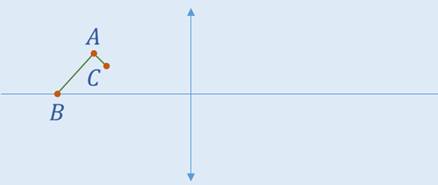
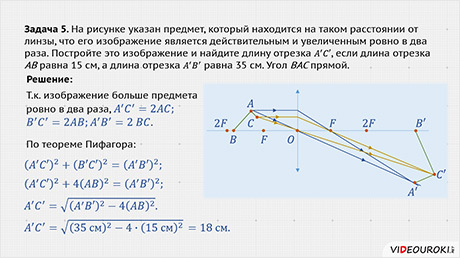
Задача 5. На рисунке указан предмет, который находится на таком расстоянии от линзы, что его изображение является действительным и увеличенным ровно в 2 раза. Постройте это изображение и найдите длину отрезка A’C’, если длина отрезка AB равна 15 см, а длина отрезка A’B’ равна 35 см. Угол BAC прямой.
РЕШЕНИЕ
Отметим на чертеже фокусы и двойные фокусы линзы. Отметим эти точки таким образом, чтобы наш предмет находился между фокусом и двойным фокусом, поскольку именно в этом случае получается действительное и увеличенное изображение (которое будет находится за двойным фокусом). Итак, чтобы построить изображение, необходимо получить изображения точек А, В и С. Построим эти точки используя два луча.
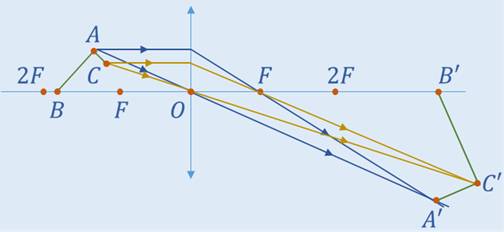
Т.к. изображение больше предмета в два раза, то


По теореме Пифагора




Ответ: 18 см.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 19934
19934

