В данной теме разберём решение задач на ход лучей в треугольной призме.
Задача 1. Луч света падает на преломляющую грань призмы под углом 30º и выходит из неё под углом 25º. При этом угол отклонения луча составляет 10º. Постройте ход лучей в призме и найдите её преломляющий угол.
|
ДАНО:
|
РЕШЕНИЕ
Угол отклонения луча определяется по формуле
Тогда преломляющий угол призмы равен
|
|
|

Задача 2. Луч света падает на преломляющую грань призмы под углом 1º. Найдите показатель преломления материала, из которого сделана призма, если преломляющий угол призмы равен 30º, а угол отклонения луча составляет 18º.
|
ДАНО:
|
РЕШЕНИЕ
Угол отклонения луча при очень малом значении угла падения
Тогда показатель преломления материала
|
|
|

Задача 3. Луч света падает на преломляющую грань призмы таким образом, что преломлённый луч внутри призмы распространяется в направлении, параллельном основанию призмы. Известно, что преломляющий угол призмы равен 50º, а угол падения равен 35º. Найдите показатель преломления материала, из которого сделана призма.
|
ДАНО:
|
РЕШЕНИЕ
Т.к. грань представленной призмы является равнобедренным треугольником и сумма углов треугольника равна 180º, то
Из построения
Тогда
Закон преломления света
|
|
|

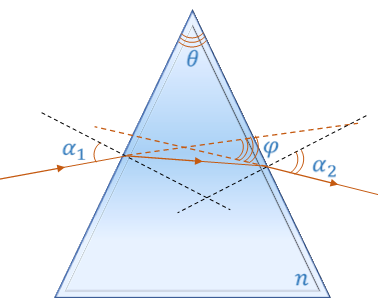
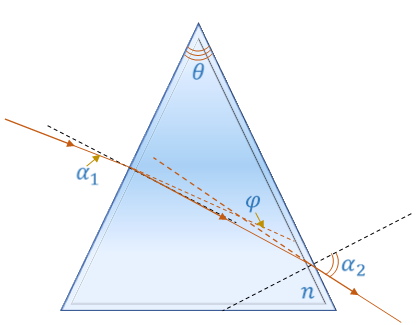
Задача 4. Луч света вошёл в призму с показателем преломления 2,4 и не вышел из неё. Найдите минимальный угол падения луча на преломляющую грань, при котором это возможно, учитывая то, перпендикуляры к преломляющим граням призмы пересекаются под углом, равным сумме преломляющего угла призмы и угла отклонения луча.
|
ДАНО:
|
РЕШЕНИЕ
Предельный угол полного отражения
Т.к. сумма углов треугольника равна 180º, то
Угол отклонения луча
Тогда
Закон преломления света
|
|
|


 Получите свидетельство
Получите свидетельство Вход
Вход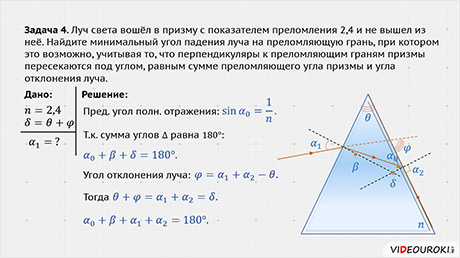














































 0
0 20667
20667

