Поговорим
о свойствах функций. Итак, напомним, что область значений функции  –
это множество всех значений функции
–
это множество всех значений функции  ,
которые она принимает при всех значениях аргумента
,
которые она принимает при всех значениях аргумента  из
области её определения
из
области её определения  .
.
Значения аргумента, при которых функция принимает значение, равное нулю, называется нулями функции.
Промежутки, на которых значения функции либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
Функцию
 называют
возрастающей на некотором промежутке, если большему значению аргумента соответствует
большее значение функции, то есть для любых
называют
возрастающей на некотором промежутке, если большему значению аргумента соответствует
большее значение функции, то есть для любых  и
и
 ,
принадлежащих промежутку, из того, что
,
принадлежащих промежутку, из того, что  ,
следует
,
следует  .
.
Функцию
 называют
убывающей на некотором промежутке, если большему значению аргумента из этого
промежутка соответствует меньшее значение функции, то есть для любых
называют
убывающей на некотором промежутке, если большему значению аргумента из этого
промежутка соответствует меньшее значение функции, то есть для любых  и
и
 ,
принадлежащих промежутку, из того, что
,
принадлежащих промежутку, из того, что  ,
следует
,
следует  .
.
Промежуток, на котором функция убывает или возрастает, называется промежутком монотонности функции.
Число
 называется
наибольшим значением функции
называется
наибольшим значением функции  на
некотором промежутке, если существует
на
некотором промежутке, если существует  из
этого промежутка, такое, что
из
этого промежутка, такое, что  ,
и для любого
,
и для любого  из
этого промежутка выполняется неравенство
из
этого промежутка выполняется неравенство  .
.
Число
 называется
наименьшим значением функции
называется
наименьшим значением функции  на
некотором промежутке, если существует
на
некотором промежутке, если существует  из
этого промежутка, такое, что
из
этого промежутка, такое, что  ,
и для любого
,
и для любого  из
этого промежутка выполняется неравенство
из
этого промежутка выполняется неравенство  .
.
Точка
 называется
точкой максимума (минимума) функции
называется
точкой максимума (минимума) функции  ,
если функция определена в самой этой точке и в некоторой окрестности точки
,
если функция определена в самой этой точке и в некоторой окрестности точки  выполняется
неравенство:
выполняется
неравенство:  (для
максимума) или
(для
максимума) или  (для
минимума).
(для
минимума).
Точки максимума и минимума называются точками экстремума функции. Значение функции в точке экстремума называется экстремумом функции.
Функция
 ,
определённая на множестве
,
определённая на множестве  ,
называется ограниченной снизу на множестве
,
называется ограниченной снизу на множестве  ,
если существует число
,
если существует число  такое,
что для любого
такое,
что для любого  выполняется
неравенство
выполняется
неравенство  .
.
Функция
 ,
определённая на множестве
,
определённая на множестве  ,
называется ограниченной сверху на множестве
,
называется ограниченной сверху на множестве  ,
если существует число
,
если существует число  ,
такое, что для любого
,
такое, что для любого  ,
выполняется неравенство
,
выполняется неравенство  .
.
Функцию,
ограниченную и сверху, и снизу на множестве  ,
называют ограниченной на этом множестве.
,
называют ограниченной на этом множестве.
Функция
 является
ограниченной на множестве
является
ограниченной на множестве  тогда
и только тогда, когда существует число
тогда
и только тогда, когда существует число  такое,
что для любого
такое,
что для любого  ,
выполняется неравенство
,
выполняется неравенство  .
.
Функция
 называется
чётной, если область её определения симметрична относительно нуля и для
любого
называется
чётной, если область её определения симметрична относительно нуля и для
любого  выполняется
равенство
выполняется
равенство  .
.
График чётной функции симметричен относительно оси ординат.
Функция
 называется
нечётной, если область её определения симметрична относительно нуля и
для любого
называется
нечётной, если область её определения симметрична относительно нуля и
для любого  выполняется
равенство
выполняется
равенство  .
.
График нечётной функции симметричен относительно начала координат.
Функция
называется периодической с периодом  ,
если
,
если  ,
где
,
где  .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание
первое. Найдите наибольшее значение функции, заданной
формулой  .
.
Решение.

Задание
второе. Найдите наименьшее значение функции, заданной
формулой  .
.
Решение.


Задание третье. Установите чётность или нечётность функций:
а)
 ,
б)
,
б)  .
.
Решение.


Задание
четвёртое. Найдите все значения  ,
при каждом из которых функция
,
при каждом из которых функция  имеет
более двух точек экстремума.
имеет
более двух точек экстремума.
Решение.





 Получите свидетельство
Получите свидетельство Вход
Вход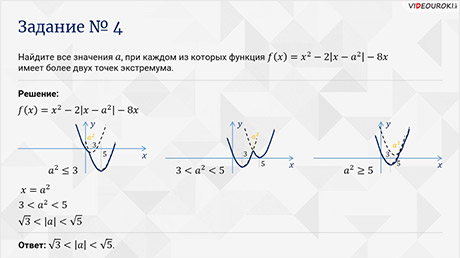




 3204
3204

