Вспомним
основные элементарные функции и рассмотрим их графики. Итак, линейная функция.
Функция 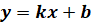 ,
где
,
где 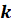 и
и
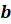 –
некоторые действительные числа, а
–
некоторые действительные числа, а 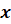 –
переменная, называется линейной.
–
переменная, называется линейной.
Область
определения линейной функции – 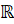 ,
область значений при
,
область значений при 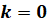 состоит
из одного числа
состоит
из одного числа 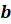 ,
при
,
при 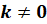 –
–
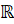 .
.
При
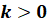 функция
возрастает, при
функция
возрастает, при 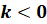 –
убывает, при
–
убывает, при 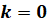 является
постоянной.
является
постоянной.
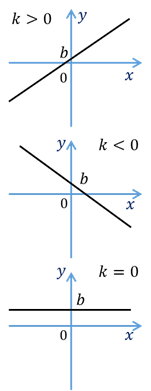
Графиком линейной функции является прямая, для её построения достаточно двух точек.
По
уравнениям линейных функций 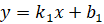 и
и
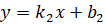 можно
судить о расположении их графиков.
можно
судить о расположении их графиков.
Если
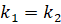 ,
то прямые параллельны; если
,
то прямые параллельны; если 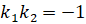 –
перпендикулярны.
–
перпендикулярны.
Угол
 между
прямыми можно найти по формуле:
между
прямыми можно найти по формуле:  .
.
Квадратичная
функция. Функция  ,
где
,
где 
 ,
,
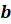 и
и
 –
действительные числа и
–
действительные числа и 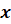 –
переменная, называется квадратичной.
–
переменная, называется квадратичной.
Областью определения квадратичной функции является множество действительных чисел.
Графиком
квадратичной функции является парабола, ветви которой при  направлены
вверх, а при
направлены
вверх, а при  –
вниз.
–
вниз.
Вершина
параболы в точке  ,
где
,
где  ,
,
 .
.
Положение
параболы относительно  зависит
от дискриминанта.
зависит
от дискриминанта.

Степенные
функции. Рассмотрим функции вида  ,
,
 ,
где
,
где  .
Область определения этих функций –
.
Область определения этих функций – 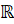 .
.
Область
значений функции  –
–
 ,
область значений функции
,
область значений функции  –
–
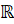 .
.
Функция
 возрастает
на всей области определения, а функция
возрастает
на всей области определения, а функция  на
промежутке
на
промежутке  убывает
и на промежутке
убывает
и на промежутке  возрастает.
возрастает.
Функция
 является
чётной, её график симметричен относительно оси ординат.
является
чётной, её график симметричен относительно оси ординат.

Функция
 является
нечётной, её график симметричен относительно начала координат.
является
нечётной, её график симметричен относительно начала координат.

Рассмотрим
функцию вида  .
.
Области определения и значений – все действительные числа, кроме нуля.
Функция
на каждом из двух промежутков области определения убывает при 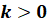 и
возрастает при
и
возрастает при 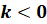 .
.
График функции называется гиперболой. Функция нечётная, график симметричен относительно начала координат.

И
рассмотрим ещё функции вида  ,
,
 ,
где
,
где  .
.
Область
определения и область значений функции  –
–
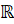 ,
а функции
,
а функции  –
–
 .
.
Обе функции возрастают на своей области определения.
Функция
 является
нечётной, её график симметричен относительно начала координат.
является
нечётной, её график симметричен относительно начала координат.

И осталось ещё вспомнить основные приёмы преобразования графиков.
Итак,
пусть дан график функции  .
.

График
функции  ,
где
,
где  ,
получается из графика функции
,
получается из графика функции  сдвигом
вдоль оси абсцисс на
сдвигом
вдоль оси абсцисс на  а
единиц влево для
а
единиц влево для  и
на
и
на  единиц
вправо для
единиц
вправо для  .
.

График
функции  ,
где
,
где  ,
получается из графика функции
,
получается из графика функции  сдвигом
его вдоль оси ординат на
сдвигом
его вдоль оси ординат на  единиц
вверх для
единиц
вверх для  и
на
и
на  единиц
вниз для
единиц
вниз для  .
.

График
функции  при
при
 получается
из графика функции
получается
из графика функции  деформацией
исходного графика
деформацией
исходного графика  вдоль
оси ординат: растяжением в
вдоль
оси ординат: растяжением в  раз
при
раз
при  или
сжатием в
или
сжатием в  раз
при
раз
при  .
.
При
 происходит
симметричное отражение графика
происходит
симметричное отражение графика  относительно
оси абсцисс, а при
относительно
оси абсцисс, а при  и
и
 происходит
отражение сначала относительно оси абсцисс с последующим необходимым
деформированием этого графика.
происходит
отражение сначала относительно оси абсцисс с последующим необходимым
деформированием этого графика.
График
функции  при
при
 получается
из графика функции
получается
из графика функции  деформацией
исходного графика вдоль оси абсцисс: сжатием в
деформацией
исходного графика вдоль оси абсцисс: сжатием в  раз
при
раз
при  или
растяжением в
или
растяжением в  раз
при
раз
при  .
.
При
 предварительно
необходимо симметрично отобразить график
предварительно
необходимо симметрично отобразить график  относительно
оси ординат, а затем осуществить необходимую деформацию этого графика.
относительно
оси ординат, а затем осуществить необходимую деформацию этого графика.
График
функции  строится
как комбинация первых двух пунктов, а именно:
строится
как комбинация первых двух пунктов, а именно:  сначала
деформируется в
сначала
деформируется в  раз,
а затем переносится на
раз,
а затем переносится на  единиц
в нужную сторону.
единиц
в нужную сторону.
График
функции  получается
из графика функции
получается
из графика функции  следующим
образом: часть графика, лежащая над осью абсцисс, остаётся без изменения, а
часть графика, находящаяся под осью абсцисс, отражается симметрично относительно
оси абсцисс. Таким образом, ниже оси абсцисс графика нет.
следующим
образом: часть графика, лежащая над осью абсцисс, остаётся без изменения, а
часть графика, находящаяся под осью абсцисс, отражается симметрично относительно
оси абсцисс. Таким образом, ниже оси абсцисс графика нет.

График
функции  получается
из графика функции и
получается
из графика функции и следующим
образом: вместо левой (относительно оси ординат) части графика изображается
отражённая (относительно оси ординат) правая. При этом правая часть графика
остаётся без изменения.
следующим
образом: вместо левой (относительно оси ординат) части графика изображается
отражённая (относительно оси ординат) правая. При этом правая часть графика
остаётся без изменения.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Функция задана графиком. Укажите область определения этой функции.

1)  2)
2)
 3)
3)
 4)
4)

Решение.


Задание второе. Укажите множество значений функции, график которой изображён на рисунке.

1)  2)
2)
 3)
3)
 4)
4)

Решение.


Задание
третье. Функция задана графиком на промежутке  .
Укажите нули этой функции.
.
Укажите нули этой функции.

Решение.


Задание четвёртое. Найдите множество значений функции, используя её график:
a)  ,
б)
,
б)  .
.
Решение.

Задание
пятое. Найдите множество значений функции  ,
используя её график.
,
используя её график.
Решение.

Задание
шестое. Укажите промежуток, которому принадлежит только один
нуль функции  :
:
1)  2)
2)
 3)
3)
 4)
4)

Решение.

Задание
седьмое. Укажите промежуток, которому принадлежат все нули
функции  .
.
1)  2)
2)
 3)
3)
 4)
4)

Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 5588
5588


