Прежде, чем познакомиться с третьим признаком подобия треугольников, вспомним известные нам первый и второй.
Итак, первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
Ну а теперь сформулируем третий признак подобия треугольников.
Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство.

 .
.
 ,
,
 ,
тогда
,
тогда  по
1-му признаку.
по
1-му признаку.
 .
.
Получаем, что  ,
,
 .
.
Тогда  по
3-му признаку.
по
3-му признаку.
Следовательно,  .
.
Так как  ,
то
,
то  .
.
Следовательно,  .
.
Что и требовалось доказать.
Давайте найдём среди следующих треугольников подобные.

У каждого из треугольников известны длин трёх его сторон, а тогда воспользуемся только что доказанным третьим признаком подобия треугольников.
Посмотрим внимательно на значения их длин и заметим, что стороны треугольника а пропорциональны сторонам треугольника в, а значит, эти треугольники подобны. При этом коэффициент подобия равен 2.
Задача. Подобны ли
треугольники  и
и
 ,
если
,
если  см,
см,
 см,
см,
 см,
см,
 см,
см,
 см,
см,
 см?
см?
Решение.

 ,
,
 ,
,
 .
.
Значит,  .
.
Следовательно,  .
.
Ответ:  .
.
Задача. Докажите, что
прямоугольные треугольники  и
и
 подобны,
если стороны
подобны,
если стороны  и
и
 треугольника
треугольника
 соответственно
равны
соответственно
равны  см
и
см
и  см,
а стороны
см,
а стороны  и
и
 треугольника
треугольника
 соответственно
равны
соответственно
равны  см
и
см
и  см.
см.
Решение.

 ,
, ,
,
 (см).
(см).
 ,
,
 ,
,
 (см).
(см).
 ;
;
 ;
;
 .
.
Значит,  .
.
Следовательно,  по
3-му признаку.
по
3-му признаку.
Что и требовалось доказать.
Итак, сегодня на уроке мы познакомились с ещё одним признаком подобия треугольников: если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Также мы закрепили материал на практике.

 Получите свидетельство
Получите свидетельство Вход
Вход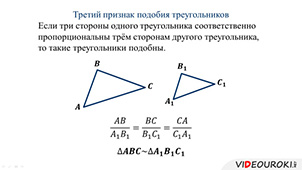



 0
0 17685
17685

