Основные понятия кинематики. Относительность движения (практика)

В данной теме будет рассмотрено решение некоторых типовых задач по кинематике.

Задача 1. Велосипедист движется по прямолинейному гладкому участку дороги. Каковы траектории движения относительно велосипедиста и относительно стоящего на обочине человека рамы велосипеда; точки на ободе колеса; точки на конце педали?

Решение:

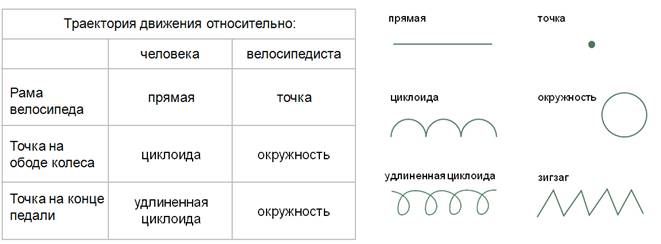
Начнем с определения вида траектории рамы велосипеда. Здесь все очень просто: так как относительно велосипедиста рама неподвижна, то траекторией ее движения будет являться точка.

Относительно же человека, стоящего на обочине дороги, рама будет двигаться прямолинейно, «вычерчивая» в воздухе прямую линию.

Теперь исследуем движение точки, располагающейся на ободе колеса, относительно велосипедиста. Представьте, что вы сели на велосипед, приметили положение ниппеля на переднем колесе и не спеша надавили на педаль, не выпуская ниппель из поля зрения. Какую траекторию описывает ниппель?..

Точка, располагающаяся на ободе колеса, относительно велосипедиста, описывает окружность. Аналогично будет себя вести и точка, находящаяся на конце педали

Теперь разберемся с траекторией движения точки на ободе колеса, относительно человека, стоящего на обочине. Вновь обратимся к мысленному эксперименту. Мы стоим на обочине, а мимо нас проезжает велосипедист. Зафиксировали взгляд на какой-либо точке колеса (пусть это будет, например, светоотражатель на конце спицы) и проследим за ее траекторией.

Получаются кривые, которые принадлежат семейству циклоид. Значит траекторией движения точки на ободе колеса относительно неподвижного человека на обочине является циклоида.

Траекторией движения точки на конце педали относительно неподвижного человека на обочине будет являться удлиненная циклоида.

Задача 2. Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца за месяц; в) длины экватора и г) скорости движения Земли по орбите вокруг Солнца?

Решение:

Тело можно принять за материальную точку, если:

1) тело движется поступательно;

2) размеры тела много меньше расстояния, которое оно проходит;

3) размеры тела много меньше расстояния до тела отсчета.

Рассмотрим вариант а более подробно. Для это проверим выполнение выше названных условий. Согласно первому условию, тело должно двигаться поступательно. Для этого случая оно не выполняется, так как о движении Земли в условии задачи ничего не говорится. Второе условие материальной точки также не выполняется, так как не известно расстояние, пройденное Землей. По третьему условию размеры тела должны быть намного меньше расстояния до тела отсчета. В данном случае, тело отсчета — это Солнце. Среднее расстояние от Земли до Солнца составляет 149,6 миллионов км, а средний радиус нашей планеты всего 6371 км, что, конечно же, намного меньше среднего расстояния до Солнца.

Следовательно, в первом примере  Землю можно принять за материальную точку, так как выполняется третье условие.

Во втором примере Землю можно принять за МТ, т. к. ее размеры много меньше расстояния, которое она проходит по орбите за месяц.

В примере «в» Землю нельзя считать МТ, т. к. при расчете длины экватора Земли нельзя пренебречь ее размерами.

В последнем примере Землю можно считать МТ, т. к. размеры Земли (радиус 6371 км) во много раз меньше расстояния до Солнца (149,6 млн. км).

Задача 3. На рисунке указаны положения точек А, О, В, С и направление оси Х. Перерисуйте рисунок и определите координаты точек, если: а) за начало отсчета принята точка О; б) за начало отсчета принята точка В.

Решение:

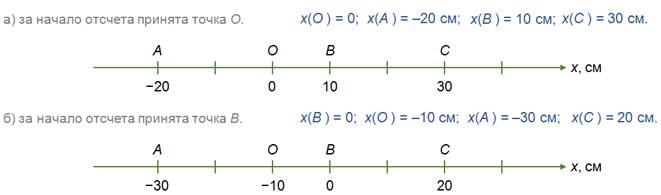
Задача 4. Мяч вертикально упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Сделайте чертеж. Найдите путь и модуль перемещения мяча.

 «Упражнение, друзья, даёт больше,

чем хорошее природное дарование».

Протагор