Равномерное прямолинейное движение. Скорость

В прошлой теме говорилось о механическом движении, которое представляет собой изменение положения тел (или частей одного и того же тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения необходимо выбрать тело отсчета, то есть тело или группу тел, которое в данном случае принимают за неподвижное и относительно которого рассматривается движение других тел, и связать с ним систему координат.

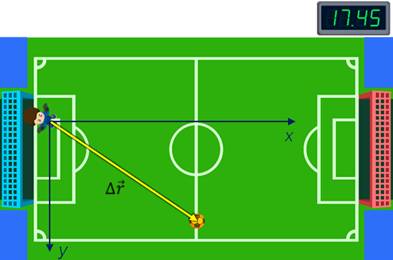
Так же было установлено, что для определения положения тела в какой-то момент времени, нужно знать вектор его перемещения. Действительно, для того, чтобы сказать, как переместилось тело, необходимо знать не только расстояние от начальной точки, но и направление, в котором тело переместилось.

Также довольно важной характеристикой любого движения является скорость. В данной теме разговор пойдёт о скорости при равномерном прямолинейном движении тела. Равномерное прямолинейное движение — это самый простой вид движения. При таком движении тело двигается только по прямой и за любые равные промежутки времени совершает равные перемещения. То есть это движение с постоянной по модулю и направлению скоростью.

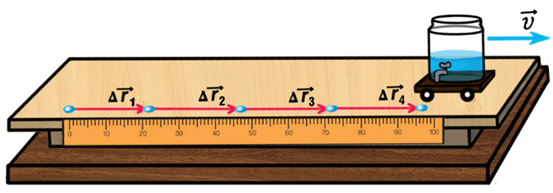
Обратите внимание на то, что всегда необходимо задавать направление скорости. В прошлых темах было показано, что выбор системы отсчёта имеет решающее значение, а в разных системах отсчета скорости могут быть направлены по-разному.

Вообще скоростью называется физическая векторная величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения. Иными словами, это производная радиус-вектора точки по времени.

Уравнение скорости для равномерного прямолинейного движения имеет вид

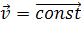
По формулам, написанным в векторном виде, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия. И так, как же рассчитать проекцию скорости? Рассмотрим простой пример. Пусть в начальный момент времени координата тела была равна x₀, а в момент времени t – x.

Тогда за промежуток времени ∆tؚ, равный tؚ - tؚ₀, координата тела изменилась на величину равную разности между конечной и начальной координатой тела. Тогда проекция скорости тела в этом случае будет равна отношению изменения координаты тела к промежутку времени, в течении которого это изменение произошло.

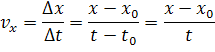
Из записанной формулы, воспользовавшись известными математическими приемами, можно получить уравнение зависимости координаты тела от времени.

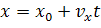
Полученное уравнение называют кинематическим уравнением равномерного движения.

Известно, что разность между начальной и конечной координатой тела есть ни что иное, как проекция перемещения на выбранную координатную ось.

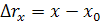
Воспользуемся основным свойством пропорции, чтобы выразить проекцию перемещения.

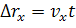
Полученное уравнение называется уравнением перемещения.

При равномерном прямолинейном движении направление вектора скорости не изменяется, а значит путь и модуль проекции перемещения тела равны. На основании этого, получим уравнение пути при равномерном прямолинейном движении тела.

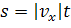
Обратите внимание, что проекция скорости тела взята под знак модуля. Это объясняется тем, что путь не может быть отрицательным, а вот знак проекции вектора скорости, как и проекции перемещения, будет зависеть от выбора направления координатной оси.

Рассмотрим графические зависимости скорости, координаты, пути и перемещения от времени при равномерном прямолинейном движении. При равномерном движении скорость постоянна, поэтому график зависимости скорости от времени будет представлять собой прямую линию, параллельную оси времени. Иными словами, при равномерном движении скорость не зависит от времени, так как является величиной постоянной.

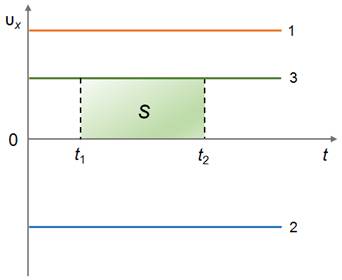
Из графика скорости видно, что проекция скорости тел для оранжевой и зелёной прямых больше нуля, так как они располагаются выше оси времени. В случае с синей прямой, наблюдается противоположная картина: значит, тело двигается в обратном направлении, поэтому проекция скорости отрицательная.

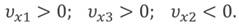
Если рассмотреть конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты «Икс», а, следовательно, пройденным телом путем. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а длина другой — это промежуток времени.

Следующим рассмотрим график зависимости проекции перемещения от времени. Для этого еще раз вспомним уравнение перемещения:

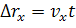
Из уравнения видим, что проекция перемещения линейно зависит от времени. Следовательно, при равномерном движении графиком перемещения является прямая линия.

Направление и угол наклона графика зависимости проекции перемещения к оси времени будет зависеть от проекции вектора скорости на координатную ось.

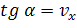
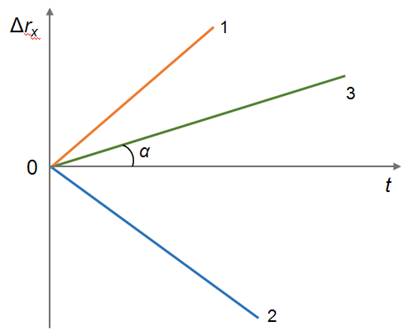
Из рисунка видно, что тело 1 и тело 3 движутся в положительном направлении оси х, при этом скорость первого тела больше скорости третьего.

Тело 2 движется в направлении, противоположном направлению оси х, поэтому график перемещения располагается под осью времени.

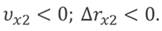
Рассмотрим зависимость пройденного пути от времени.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, так как зависимость пути от времени, как и в случае с перемещением тела, линейная. Однако графики зависимости пути от времени для всех трех тел располагаются выше оси времени. Это объясняется тем, что пройденный путь — это длина траектории, а, следовательно, путь не может быть отрицательным.

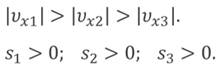
Наклон графика пути к оси времени, как и в случае с графиком перемещения, зависит от модуля скорости: чем больше скорость движения тела, тем больший угол наклона.

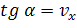
Рассмотрим графики зависимости координаты от времени (их еще называют графиками движения).

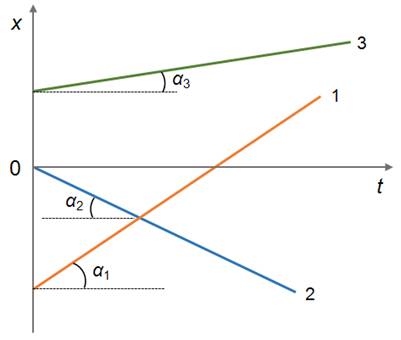
На рисунке представлены три прямые, каждая из которых описывается одним и тем же уравнением. Точки пересечения этих графиков с осью x соответствуют значениям начального положения. Как видно из графика, для первого тела x₀<0, для второго x₀=0, а для третьего — x₀>0.

Так же на графике хорошо видно, что проекции скоростей для первого и третьего тел больше нуля. Действительно, ведь значение координаты x увеличивается с течением времени. Значит, тело двигается в направлении, совпадающем с положительным направлением оси икс. Это соответствует положительному перемещению, а, значит, положительной проекции скорости.

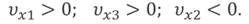
В случае с синей прямой, наблюдается противоположная картина: значит второе тело двигается в обратном направлении, поэтому его проекция скорости отрицательная.

Кроме того, из графиков можно судить о модуле скорости. Очевидно, что тело, движение которого описано оранжевой прямой, двигается быстрее остальных, так как за один и тот же промежуток времени оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что модуль скорости второго тела больше, чем модуль скорости тела номер три.

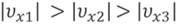
При этом, как и в случае с перемещением, угол наклона графика к оси времени зависит от скорости тела. Из этих наблюдений можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем больше скорость движения тела.

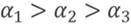
В случае прямолинейного равномерного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).

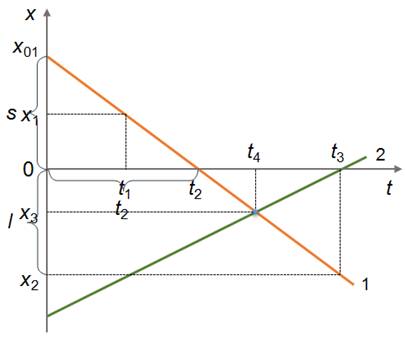
С помощью графика движения можно определить:

1) координаты тела в любой момент времени;

2) путь, пройденный телом за некоторый промежуток времени;

3) время, за которое пройден какой-то путь;

4) кратчайшее расстояние между телами в любой момент времени;

5) момент и место встречи тел;

6) и так далее.

Необходимо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

Очень часто наблюдаются довольно сложные типы движения, когда тело движется относительно системы отсчёта, которая в тоже время движется относительно Земли. На прошлых уроках говорилось о том, что любое механическое движение относительно, то есть в разных системах отсчета будут различны вид траектории, значение скорости, перемещения и других физических величин.

Было установлено, что в случае, когда тело участвует одновременно в нескольких движениях, результирующее перемещение тела равно векторной сумме перемещений, совершаемых им в каждом из движений.

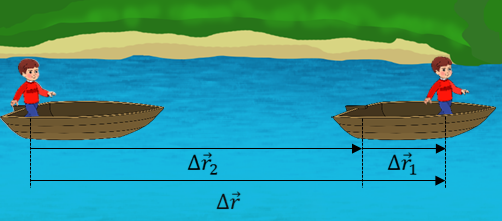
В рассматриваемом примере очевидно, что все перемещения произошли за один и тот же промежуток времени. Разделив каждое перемещение в уравнении на этот промежуток времени, получим классический закон сложения скоростей, установленный Галилеем: скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.

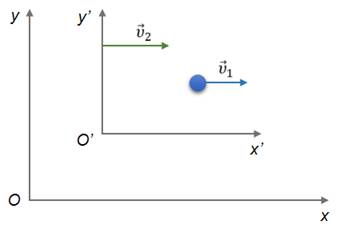
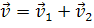
Здесь следует помнить, что данный закон справедлив и для неравномерного движения. В этом случае вектора скорости — это мгновенные скорости, то есть скорости в данный момент времени или в данной точке траектории.

Основные выводы:

В данной теме были повторены некоторые важные понятия кинематики. Поговорили о равномерном прямолинейном движении тел и способах описания такого движения. Еще раз затронули относительность движения и вывели классический закон сложения скоростей.