Основные понятия кинематики. Относительность движения

С данной темы приступаем к повторению первого раздела физики, который называется «Кинематика». И в начале вспомним основные понятия, относящиеся к данному разделу, а также поговорим об относительности движения.

Кинематика, как часть механики, была известна еще со времен Аристотеля. Однако впервые раздел кинематики был четко выделен в курсе «Физической и экспериментальной механики» генерала Жана-Виктора Понселе, который читал его в Парижском университете с 1837 по 1848 годы.

Кинематика — это раздел механики, в котором изучают движение тел, без рассмотрения причин, вызвавших это движение.

Основной задачей кинематики является нахождение положения тела в произвольный момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Наиболее простым видом движения в природе является механическое движение. Под механическим движением понимают изменение положения тел (или частей одного тела) друг относительно друга в пространстве с течением времени.

Простым примером механического движения может служить лодка, плывущая по реке. Она меняет свое положение относительно берега, деревьев и человека, находящихся на берегу. И таких примеров можно привести достаточно много.

Чтобы изучать движение тела, нужно прежде всего уметь определять это положение. Здесь важно помнить, что положение тела можно задать только относительно какого-либо другого тела, которое, обычно, называют телом отсчета. И так, тело отсчета — это тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Тело отсчета можно выбрать совершенно произвольно. В рассмотренном примере, им может служить рыбак, стоящий на берегу реки, или деревья, кусты, береговая линия.

Для описания движения мало выбрать тело отсчета, необходимо еще указать и систему координат, связав ее с телом отсчета, и способ измерения времени. Так вот, совокупность тела отсчета, системы координат и способа измерения времени создают систему отсчета, относительно которой и рассматривают движение тела.

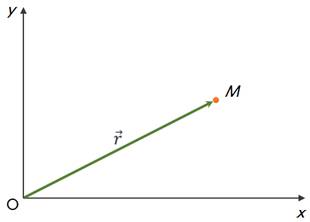
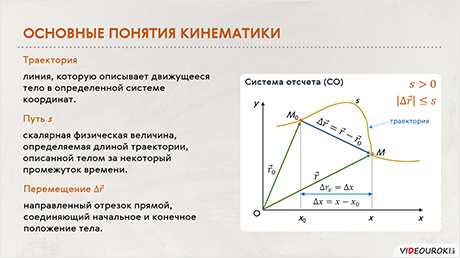
Положение тела в пространстве можно определить с помощью радиус-вектора или при помощи координат. Радиус-вектор — это вектор, который соединяет исследуемую точку и начало координат. Радиус-вектор обозначается латинской буквой  и, как и любой другой вектор, имеет длину и направление.

Под координатой точки понимают проекцию конца радиус-вектора на выбранную координатную ось.

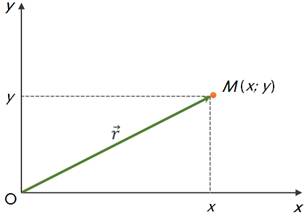
Таким образом, для того, чтобы в рассмотренном примере определить координату точки М, необходимо опустить с конца радиус-вектора два перпендикуляра — на ось Ox и ось Oy. Тогда найденные значения x и y и будут являться координатами точки M.

Еще одно затруднение, с которым можно столкнуться, при изучении движения тела, это то, что каждое тело имеет определенные размеры, следовательно, разные его части, разные точки тела находятся в разных местах простран­ства. Так как же определить положение всего тела? В общем слу­чае это сделать трудно. Но оказывается, во многих случаях нет необхо­димости указывать положение каждой точки движущего­ся тела.

Зачем, например, описывать движение каждой точки самолета, если эти движения ничем не различаются между собой?

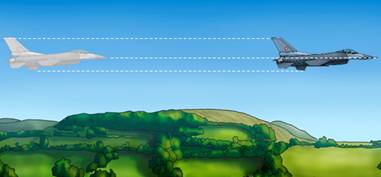
Движение тела, при котором все его точки движутся одина­ково, называют поступа­тельным.

Не нужно описывать движение каждой точки тела и тогда, когда размеры тела малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до дру­гих тел.

На­пример, сидя в автомобиле, его нельзя считать точкой, по отношению к водителю или пассажиру, но, например, автомобиль мал по сравнению с протяженностью расстояния, которое ему предстоит преодолеть, и поэтому автомобиль считают точкой при описании его движения.

Так же поступают в астрономии при изучении движений небесных тел. Планеты, звезды и Солнце, конечно, не малые тела.

Но, например, в сравнении с масштабами нашей галактики «Млечный путь» и Землю и Солнце мы можем принимать за точку, которая движется вокруг другой точки — центра галактики.

А можно ли галактику принять за точку? Конечно же да, но только в случаях рассмотрения ее движения относительно других галактик или всей Вселенной.

Поэтому говоря в дальнейшем о движении тела, в действительности будем иметь в виду движение какой-нибудь точки этого тела. Не надо забывать при этом, что эта точка ма­териальна, то есть она отличается от обычных тел лишь тем, что она не имеет размеров.

Таким образом, материальная точка — это тело, размерами которого в данных условиях движения можно пренебречь.

Линия, которую описывает движущееся тело в определенной системе координат, называется траекторией. Например, в идеализированной модели движения Луны вокруг Земли, в системе отсчета, связанной с Землей, траекторией движения Луны будет являться окружность.

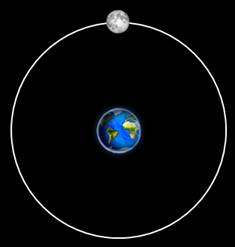
А в системе отсчета, связанной с Солнцем это кривая, чем-то напоминающая лепестки цветка (такую кривую еще называют циклоидой).

Если можно найти длину траектории, которую описало тело за некоторый промежуток времени, то можно определить путь, пройденный телом. Обозначается путь малой латинской буквой s. Следует также помнить, что путь — величина скалярная и всегда положительная.

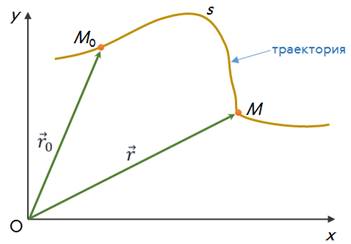
В тех случаях, когда траектория движения не известна, определить положение тела, то есть его координаты, в конце пути нельзя, даже если известны начальное положение тела и длина пройденного им пути.

Допустим, известно, что некоторое тело начинает двигаться из точки О и за один час проходит 20 км.

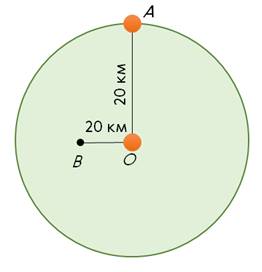
Для ответа на вопрос, где будет находиться тело спустя один час после его выхода из точки О, не хватает информации о его движении. Ведь тело могло, например, двигаться прямолинейно в северном направлении и оказаться в точке А, находящейся на расстоянии 20 км. А могло также, дойдя до точки B, находящейся на расстоянии 10 км от точки О, повернуть на восток и вернуться в точку О. При этом пройденный путь также окажется равным 20 км. При заданном значении пути, тело могло оказаться в любой точке пространства, ограниченного окружностью, радиуса 20 км.

Чтобы избежать такой неопределенности, для нахождения положения тела в пространстве в заданный момент времени, была введена физическая величина, называемая перемещением.

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением.

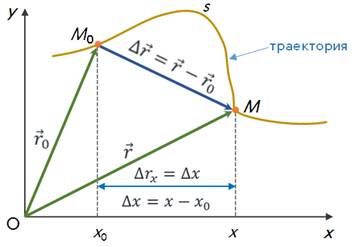
Как видно из рисунка, перемещение тела равно геометрической разности радиус-векторов тела в начальный и конечный моменты времени.

Для того, чтобы определить проекцию перемещения на выбранную координатную ось, необходимо найти координаты тела в начальный и конечный моменты времени, и найти их разность.

Необходимо отметить, что модуль перемещения не может быть больше пути.

Знак равенства относится только к случаю прямолинейного движения, если направление движения не изменяется.

Скорость — это мера механического состояния тела, которая характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Известно, что тело в редких случаях движется с неизменной скоростью, поэтому для характеристики такого движения было введено понятие средней скорости. И так, средняя скорость — это векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения.

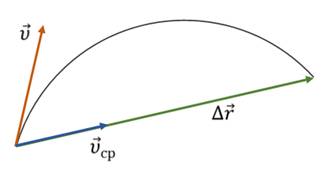
Так же в физике различают понятие мгновенной скорости, то есть скорости тела в данный момент времени или в данной точке траектории. Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени.

 – это производная от радиус-вектора по времени.

Следует помнить, что мгновенная скорость всегда направлена по касательной к траектории движения тела, а в случае прямолинейного движения совпадает с ней.

Следующей важной характеристикой движения является ускорение. Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

Среднее ускорение — векторная физическая величина, численно равная отношению изменения скорости ко времени, за который оно произошло.

где  — это производная от скорости по времени.

Для того, чтобы найти направление вектора среднего ускорения, необходимо найти направление вектора изменения скорости. Для этого параллельным переносом совмещают начало вектора начальной скорости с началом вектора конечной скорости и строят их разность.

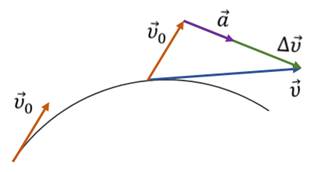
Вектор среднего ускорения направлен параллельно вектору скорости в сторону вогнутости траектории.

Важно запомнить, что, зная траекторию движения тела, можно определить направление вектора его скорости, но не ускорения. Ведь направление ускорения определяется направлением равнодействующей сил, действующих на тело.

На рисунке изображен автомобиль. Что можно сказать о данном автомобиле: движется он или покоится? Однозначного ответа нет. Ведь не известно, относительно чего рассматривать его движение.

А вот так?

Здесь можно сказать, что автомобиль движется относительно дороги.

А что можно сказать о водителе данного автомобиля: он движется или покоится?

В данном примере оба ответа будут правильными, ведь относительно дороги водитель действительно движется вместе с автомобилем, а относительно автомобиля он покоится.

А что можно сказать о траектории его движения? И опять здесь нет однозначного ответа.

Так как в разных системах отсчета будут различны вид траектории, значение скорости и других величин! В этом и заключается относительность движения.

Вот еще один пример. Два велосипедиста на велосипеде-тандеме движутся по проселочной дороге. Движутся ли они относительно друг друга?

Правильный ответ — «нет», так как положение их тел относительно друг друга не меняется с течением времени.

А вот еще один классический пример. Мальчик переходит с кормы на нос лодки, которая сама движется по течению реки. Когда мальчик доходит до носа лодки, отсчет времени прекращают. Каково перемещение мальчика относительно берега реки?

Для ответа на этот вопрос необходимо определить перемещение мальчика, относительно лодки.

И перемещение лодки относительно берега, за этот промежуток времени.

Тогда очевидно, что перемещение мальчика относительно берега будет равно геометрической сумме перемещений мальчика относительно лодки, и лодки, относительно берега.

Таким образом, если тело одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. В этом состоит установленный экспериментально принцип независимости движений.

Основные выводы:

В рамках данной темы были повторены основные понятия кинематики, поговорили о механическом движении тел и способах его описания. А также разобрались с понятием относительности механического движения.