Получите свидетельство
Вход
Вы уже знакомы с основным свойством дроби. Давайте вспомним его:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.
Иначе говоря, при любых a, b и c верны равенства
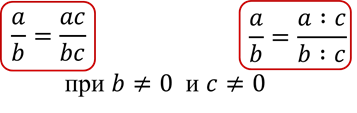
Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.
Равенство,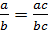 
справедливо и не только при натуральных, но и
при любых значениях переменных a, b и c
при которых знаменатель не равен нулю.
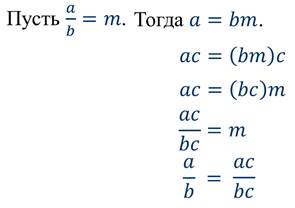
Рациональные дроби тоже можно преобразовывать таким же образом.
Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.
Основное свойство рациональной дроби сводится к тому, что:
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Например
Это равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.
Определение:
Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.
Замену одного такого выражения другим называют тождественным преобразованием выражения.
Равенство
Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.
Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.
Задание
Сократить дробь.
Решение:
Задание
Привести дробь к указанному знаменателю.
Решение:
Итоги:
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.
0
18762
