Сегодня на уроке мы напомним, что называют криволинейной трапецией. Вспомним, как можно вычислить её площадь. Рассмотрим применение интеграла для вычисления площадей.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним,
что криволинейной трапецией называют фигуру, ограниченную снизу отрезком
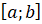 оси
оси 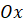 , сверху графиком непрерывной функции
, сверху графиком непрерывной функции 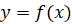 такой, что
такой, что 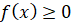 при
при 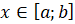 и
и 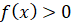 при
при 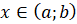 , а с боков ограниченную отрезками прямых
, а с боков ограниченную отрезками прямых 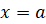 и
и 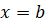 . Отрезок
. Отрезок 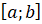 называют основанием этой криволинейной трапеции.
называют основанием этой криволинейной трапеции.
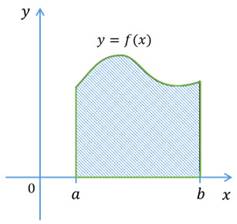
Площадь криволинейной трапеции можно
вычислить по формуле 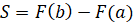 , где
, где 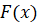 – любая первообразная функции
– любая первообразная функции 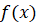 .
.
Вспомним формулу Ньютона – Лейбница: 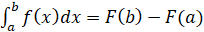 . Помним, что данная формула может быть записана и вот таким
образом:
. Помним, что данная формула может быть записана и вот таким
образом: 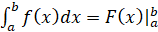 .
.
Таким образом, из двух формул получаем, что 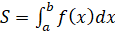 .
.
На одном из предыдущих занятий мы с вами решали задачи на вычисление площади криволинейной трапеции.
Давайте сейчас вычислим площадь криволинейной трапеции,
ограниченной 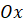 , прямыми
, прямыми 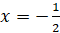 ,
, 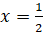 и параболой
и параболой 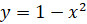 .
.

Теперь вычислим площадь криволинейной трапеции, ограниченной осью 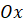 , прямыми
, прямыми  ,
,  и графиком функции
и графиком функции  .
.

Далее найдём площадь фигуры, ограниченной параболами  ,
,  и осью
и осью 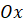 .
.

Давайте найдём площадь криволинейной трапеции ограниченной прямыми
 ,
,  , осью
, осью 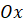 и графиком функции
и графиком функции  .
.

Теперь найдём площадь фигуры, ограниченной отрезком  оси
оси 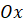 и графиком функции
и графиком функции  на этом отрезке.
на этом отрезке.

Запомните, что если  на отрезке
на отрезке 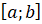 , причём равенство нулю может быть лишь на его концах, то площадь
, причём равенство нулю может быть лишь на его концах, то площадь  криволинейной трапеции равна
криволинейной трапеции равна  .
.
Далее давайте найдём площадь фигуры, ограниченной параболой  и
и  .
.
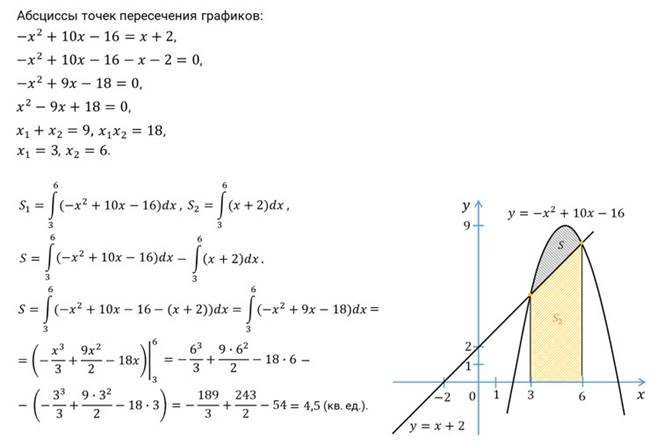
Посмотрите на фигуру, изображённую на следующем рисунке.

Её площадь равна разности двух трапеций, опирающихся на отрезок 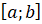 . Сверху первая трапеция ограничена графиком функции
. Сверху первая трапеция ограничена графиком функции  . Вторая трапеция сверху ограничена графиком функции
. Вторая трапеция сверху ограничена графиком функции  .
.
Площадь этой фигуры равна  . Эта формула справедлива для любых непрерывных функций
. Эта формула справедлива для любых непрерывных функций  и
и  (принимающих значения любых знаков), удовлетворяющих условию
(принимающих значения любых знаков), удовлетворяющих условию  .
.
Найдём площадь фигуры, ограниченной параболами  и
и  .
.


 Получите свидетельство
Получите свидетельство Вход
Вход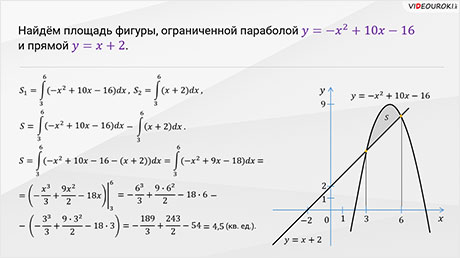




 3208
3208


