Вопросы занятия:
· расстояние от точки до плоскости;
· расстояние между параллельными плоскостями;
· расстояние между прямой и параллельной ей плоскостью;
· расстояние между скрещивающимися прямыми.
Материал урока.
Вы уже знаете, что расстоянием от точки до прямой называют длину перпендикуляра проведённого из данной точки к данной прямой. Ведь длина этого перпендикуляра наименьшая среди длин всевозможных отрезков, проведённых из данной точки к данной прямой.
Рассмотрим случай точки и плоскости.
Понятно, что если точка лежит в плоскости, то расстояние между ними равно нулю. Что же на счет случая, когда точка не лежит в плоскости?
Итак, точку с плоскостью можно соединить различными способами. Но среди всех возможных проведённых отрезков можно выделить один особенный. Тот, который перпендикулярен к данной плоскости.
Давайте рассмотрим отрезок перпендикулярный к плоскости и любой из оставшихся.
Если соединить точки пересечения данных отрезков с плоскостью, то тем самым получим треугольник, причём он будет являться прямоугольным.
Действительно, если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой из этой плоскости.
Введём несколько новых понятий.
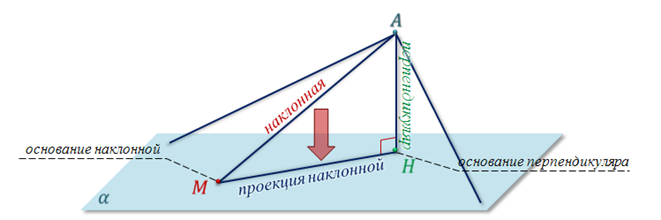
Запомните, отрезок AH называют перпендикуляром, проведённым из точки А к плоскости α, а точку H — основанием перпендикуляра.
Отрезок AM называю наклонной к плоскости, а точку M — основанием наклонной.
Отрезок HM называют проекцией наклонной на плоскость α.
Понятно, что гипотенуза всегда длиннее любого из катетов. Тогда можем сделать вывод, что перпендикуляр, проведённый из данной точки к плоскости, меньше любой наклонной, проведённой из той же точки к этой плоскости.
Тем самым можно утверждать, что расстоянием от точки А до плоскости α является длина перпендикуляра, проведённого из точки А к плоскости α.
Основываясь на этом определении, получим несколько замечаний. Первым рассмотрим расстояние между параллельными плоскостями.
Рассмотрим параллельные плоскости α и β. В плоскости α отметим две произвольные точки А и B. И проведём перпендикуляры из этих точек к плоскости β.
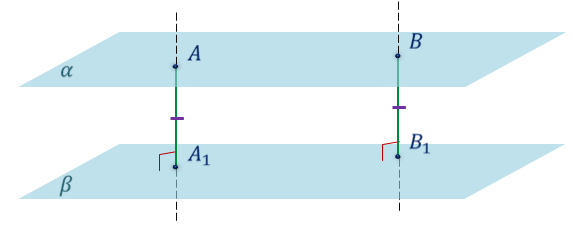
Мы получили отрезки AA1 и BB1. Каждый из них перпендикулярен плоскости β, а значит, АА1 параллельно BB1.
Вам уже известно, что отрезки параллельных прямых, заключенных между параллельными плоскостями, равны.
Можно сказать, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
Запишем замечание. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Хорошим примером может служить расстояние между плоскостями пола и потолка комнаты. Все точки потолка находятся на одинаковом расстоянии от пола, это расстояние и является высотой комнаты.

Рассмотрим следующий случай, расстояние между прямой и параллельной ей плоскостью.
В данном случае на прямой нужно выбрать некоторую точку и провести перпендикуляр к плоскости. Ведь понятно, что все точки прямой равноудалены от данной плоскости.

Таким образом, можем записать, что расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Нам осталось рассмотреть две скрещивающиеся прямые. Ранее уже было доказано, что через одну из скрещивающихся прямых можно провести плоскость параллельную другой прямой и притом только одну. А определение расстояния между прямой и плоскостью нам уже известно.

Тогда можно сказать, что расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Решим несколько задач.
 Доказательство.
Доказательство.
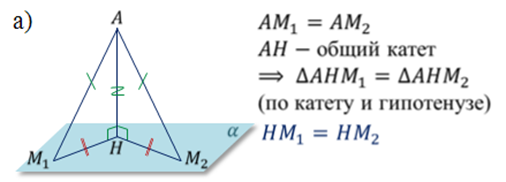


Что и требовалось доказать.
Решим ещё одну задачу.
Задача.
 перпендикуляр
к плоскости
перпендикуляр
к плоскости ,
,
 наклонные
к плоскости
наклонные
к плоскости  .
.
 ,
,
 см.
см.
Найти расстояние между основаниями наклонных.
Решение.
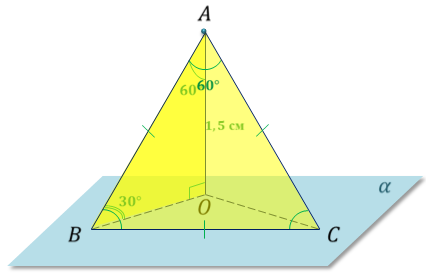

Ответ. 3 см.
Подведём итоги нашего урока.
Сегодня мы ввели такие понятия, как «перпендикуляр к плоскости», «наклонная к плоскости», «основание перпендикуляра» и «основание наклонной», а также «проекция наклонной на плоскость».
В ходе решения задач мы доказали, что: если наклонные равны, то равны и их проекции; если проекции наклонных равны, то равны и наклонные; если наклонные не равны, то большая наклонная имеет большую проекцию.
Также мы сформулировали определение понятия расстояния от точки до плоскости.
Расстоянием от точки А до плоскости α является длина перпендикуляра, проведённого из точки А к плоскости α.
Опираясь на это определение, мы сделали следующие замечания.
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Все определения и утверждения, с которыми вы познакомились на этом уроке, очень пригодятся в дальнейшем изучении стереометрии.

 Получите свидетельство
Получите свидетельство Вход
Вход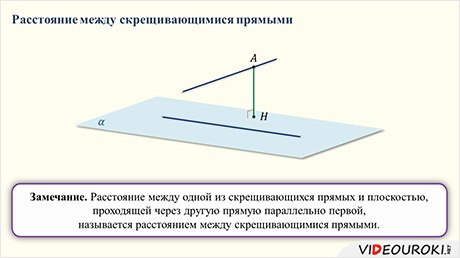



 1
1 11340
11340


как скачать