Вопросы занятия:
· сформулируем теорему о трех перпендикулярах и докажем ее;
· сформулируем и докажем обратную теорему.
Материал урока.
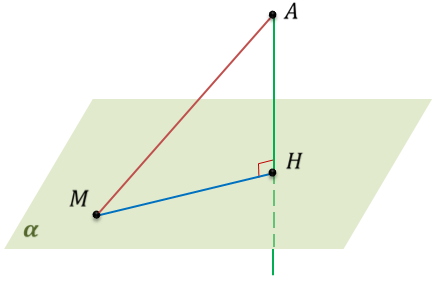
Напомню, что перпендикуляром, проведенным из точки А к плоскости α, называется отрезок AH. Точка AH называется основанием перпендикуляра. Если точка M – произвольная точка плоскости α, отличная от точки AH, то отрезок AM называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Проекцией наклонной на плоскость, называется отрезок, соединяющий основание перпендикуляра и основание наклонной, проведенных из одной и той же точки к данной плоскости. В нашем случае, отрезок HM является проекцией наклонной AM на плоскость α.
Рассмотрим пример. Пусть ABCA1B1C1 – прямая треугольная призма. Тогда ребро B1B есть перпендикуляр, проведенный из точки B1 к плоскости ее основания ABC, отрезок B1C – наклонная, отрезок CB – проекция наклонной B1C на плоскость ABC.

Давайте сформулируем и докажем теорему, которая играет важную роль при решении многих задач.
Теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Доказательство. Пусть нам дана плоскость α. Проведем перпендикуляр AH к плоскости α. Тогда AM – наклонная, точка М – основание наклонной. HM – проекция наклонной AM на плоскость α. В плоскости α проведем прямую а через основание наклонной M перпендикулярно проекции HM. Докажем, что прямая а перпендикулярна и наклонной AM.

Прямая AH – это перпендикуляр к плоскости α по условию. Значит, прямая AH перпендикулярна и всем прямым, лежащим в этой плоскости. А тогда прямая AH перпендикулярна и прямой а, лежащей в плоскости α.
Прямая HM перпендикулярна прямой а по условию. Следовательно, прямая а перпендикулярна двум пересекающимся прямым AH и HM плоскости AHM. Тогда по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости AHM. Значит, прямая а перпендикулярна любой прямой, лежащей в плоскости AHM. Прямая AM лежит в плоскости AHM. Следовательно, прямая а перпендикулярна прямой AM. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами AH, HM и AM.
Что и требовалось доказать.
Справедлива также и обратная теорема. Сформулируем и докажем ее.
Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Доказательство. Пусть нам дана плоскость альфа. Проведем перпендикуляр AH к плоскости α. Тогда прямая AM – наклонная. HM – проекция наклонной AM на плоскость α. В плоскости α проведем прямую а через основание наклонной M перпендикулярно наклонной AM. Докажем, что прямая а перпендикулярна проекции HM.

Прямая AH – это перпендикуляр к плоскости α по условию. Значит, прямая AH перпендикулярна и всем прямым, лежащим в этой плоскости. А тогда прямая AH перпендикулярна прямой а. Прямая AM перпендикулярна прямой а по условию. Следовательно, прямая а перпендикулярна двум пересекающимся прямым AH и AM плоскости AHM. Тогда по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости AHM. Значит, прямая а перпендикулярна любой прямой, лежащей в этой плоскости. Прямая HM лежит в плоскости AHM. Следовательно, прямая а перпендикулярна прямой HM. Теорема доказана.
Замечание. В доказанной прямой и обратной теореме точка М (основание наклонной) лежала на прямой а, принадлежащей плоскости α. Давайте проведем в плоскости α другую прямую b, которая параллельна прямой а. Тогда углы между прямыми b, АМ, HМ не изменятся. И из перпендикулярности прямой b и прямой AМ будет вытекать перпендикулярность прямой b и HМ и наоборот.

Решим несколько задач на применение теоремы о трех перпендикулярах.
Задача. В 
 , а
, а  –
перпендикуляр к плоскости
–
перпендикуляр к плоскости  .
Докажите, что
.
Докажите, что  – прямоугольный.
– прямоугольный.
Доказательство.
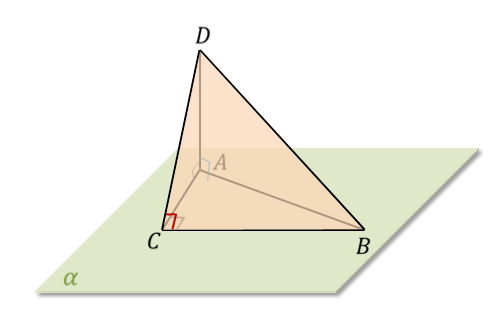

Что и требовалось доказать.
Задача.  –
куб. Точка
–
куб. Точка  –
точка пересечения диагоналей грани
–
точка пересечения диагоналей грани  .
Точка
.
Точка  –
середина ребра
–
середина ребра  .
Докажите, что
.
Докажите, что  .
.
Доказательство.


Что и требовалось доказать.
Задача. Из вершины  прямоугольника
прямоугольника
 восстановлен
перпендикуляр
восстановлен
перпендикуляр  к
плоскости прямоугольника. Расстояния от точки
к
плоскости прямоугольника. Расстояния от точки  до
остальных вершин прямоугольника равны
до
остальных вершин прямоугольника равны  см,
см,  см и
см и
 см.
Найдите длину перпендикуляра
см.
Найдите длину перпендикуляра  .
.
Решение.

 Ответ. 2 см.
Ответ. 2 см.
Подведем итоги урока. На этом уроке мы сформулировали теорему о трех перпендикулярах:прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной, и доказали ее. Сформулировали и доказали обратную теорему: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции. А также решили несколько задач на применение теоремы о трех перпендикулярах.

 Получите свидетельство
Получите свидетельство Вход
Вход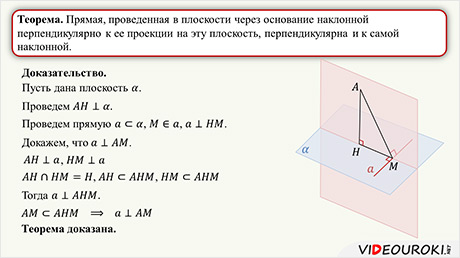



 0
0 15323
15323

