На этом уроке мы рассмотрим возможные случаи взаимного расположения сферы и плоскости в пространстве.
Прежде чем приступить к новой теме, давайте вспомним, что такое сфера.
Итак, сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Причём, данная точка называется центром сферы, а данное расстояние – радиусом сферы.

В прямоугольной
системе координат уравнение сферы радиуса  с центром в точке
с центром в точке  имеет вид:
имеет вид:

В курсе планиметрии мы с вами рассматривали три случая взаимного расположения прямой и окружности, в зависимости от соотношения расстояния от центра окружности до прямой и радиуса окружности. Вспомним их:
1) Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

2) Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.

3) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

В стереометрии же можно рассмотреть взаимное расположение сферы и плоскости в пространстве.
Итак, давайте исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.
Для этого введём следующие обозначения. Обозначим
радиус сферы буквой  ,
центр сферы буквой
,
центр сферы буквой  ,
а расстояние от её центра до некоторой плоскости альфа – буквой
,
а расстояние от её центра до некоторой плоскости альфа – буквой  .
.

Введём систему координат  .
Затем построим плоскость
.
Затем построим плоскость  ,
совпадающую с плоскостью
,
совпадающую с плоскостью  .
.
Изобразим сферу с центром в точке  ,
лежащей на положительной полуоси
,
лежащей на положительной полуоси  .
.

Обратите внимание, в этой системе координат
точка  ,
где
,
где  –
расстояние (перпендикуляр) от центра сферы до плоскости
–
расстояние (перпендикуляр) от центра сферы до плоскости  .
.
Отсюда получаем, что сфера имеет уравнение:

Плоскость  же
совпадает с координатной плоскостью
же
совпадает с координатной плоскостью  ,
а значит, её уравнение имеет вид:
,
а значит, её уравнение имеет вид:  .
.
Если координаты какой-нибудь точки  удовлетворяют
обоим уравнениям, то точка
удовлетворяют
обоим уравнениям, то точка  лежит
как в плоскости
лежит
как в плоскости  ,
так и на сфере, т. е. является общей точкой плоскости и сферы.
,
так и на сфере, т. е. является общей точкой плоскости и сферы.
Если же система этих двух уравнений не имеет решений, то сфера и плоскость не имеют общих точек.
Таким образом, вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений:

Подставим  во
второе уравнение. Преобразуем его, тогда получим следующее уравнение:
во
второе уравнение. Преобразуем его, тогда получим следующее уравнение:

Следовательно, в зависимости от соотношения  –
расстояния от центра сферы до плоскости
–
расстояния от центра сферы до плоскости  и
и
 –
радиуса сферы возможны три случая взаимного расположения сферы и плоскости в
пространстве.
–
радиуса сферы возможны три случая взаимного расположения сферы и плоскости в
пространстве.
Рассмотрим первый случай. Если  .
.

Тогда  ,
и наше уравнение:
,
и наше уравнение:  является
уравнением окружности радиуса
является
уравнением окружности радиуса  с
центром в точке
с
центром в точке  на
плоскости
на
плоскости  .
.
Координаты любой точки  этой
окружности удовлетворяют как уравнению плоскости
этой
окружности удовлетворяют как уравнению плоскости  ,
так и уравнению сферы, т. е. все точки этой окружности являются общими
точками плоскости и сферы.
,
так и уравнению сферы, т. е. все точки этой окружности являются общими
точками плоскости и сферы.
Таким образом, в данном случае сфера и плоскость пересекаются по окружности.
Сделаем вывод. Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность.
Понятно, что сечение шара плоскостью есть круг. С приближением секущей плоскости к центру шара радиус сечения (круга) увеличивается.

Тогда расстояние от центра сферы до секущей плоскости равно нулю, а в сечении получается круг, радиус которого равен радиусу шара.
Определение:
Плоскость, проходящая через диаметр шара, называется диаметральной.

А круг, полученный в результате сечения, называется большим кругом шара.

Если же секущая плоскость не проходит через
центр шара, то расстояние от центра сферы до секущей плоскости  и
и
 .
.

Очевидно, что тогда радиус сечения будет меньше радиуса сферы.
Рассмотрим второй случай. Если  .
.

Тогда  ,
и уравнению
,
и уравнению  удовлетворяют
только числа
удовлетворяют
только числа  и
и
 .
Следовательно, только координаты точки
.
Следовательно, только координаты точки  удовлетворяют
обоим уравнениям, значит,
удовлетворяют
обоим уравнениям, значит,  –
единственная общая точка сферы и плоскости.
–
единственная общая точка сферы и плоскости.
Сделаем вывод: если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.
И рассмотрим третий случай. Если  .
.

Тогда  ,
и значит, уравнению
,
и значит, уравнению  не
удовлетворяют координаты никакой точки.
не
удовлетворяют координаты никакой точки.
Сделаем вывод, если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
Задание: отрезок  –
высота тетраэдра
–
высота тетраэдра  .
Выясните взаимное расположение сферы радиуса
.
Выясните взаимное расположение сферы радиуса  с
центром
с
центром  и
плоскости
и
плоскости  ,
если:
,
если:
а)  см,
см,
 мм;
б)
мм;
б)  дм,
дм,
 см;
в)
см;
в)  см,
см,
 см.
см.
Решение: чтобы выяснить взаимное расположение сферы и плоскости, мы должны рассмотреть соотношение расстояния от центра сферы до плоскости и радиус сферы.

В первом пункте, расстояние от центра сферы до
плоскости  больше радиуса сферы.
больше радиуса сферы.

Следовательно, сфера и плоскость не имеют общих точек, и значит, не пересекаются.
Во втором пункте, расстояние от центра сферы
до плоскости  меньше радиуса сферы.
меньше радиуса сферы.

Значит, сфера и плоскость пересекаются по окружности.
И в последнем пункте, расстояние от центра
сферы до плоскости  равно радиусу сферы.
равно радиусу сферы.

А это говорит о том, что сфера и плоскость имеют только одну общую точку или иначе говоря, плоскость касается сферы.
Задача: шар пересечён
плоскостью. Площадь сечения равна  см2.
Расстояние от центра шара до плоскости сечения равно
см2.
Расстояние от центра шара до плоскости сечения равно  см.
Найдите радиус шара.
см.
Найдите радиус шара.
Решение: сечение шара плоскостью – круг, центр которого совпадает с основанием перпендикуляра, опущенного из центра шара на плоскость сечения.

Значит, из центра шара О проведём
перпендикуляр  .
Затем соединим точки
.
Затем соединим точки  и
и
 .
Получим прямоугольный треугольник
.
Получим прямоугольный треугольник  ,
у которого гипотенуза
,
у которого гипотенуза  .
.
По условию задачи  см,
см,
 см2.
Так как площадь круга
см2.
Так как площадь круга  ,
то получаем, что радиус сечения равен
,
то получаем, что радиус сечения равен  (см).
(см).
Из прямоугольного треугольника  по
теореме Пифагора находим:
по
теореме Пифагора находим:  (см).
Запишем ответ.
(см).
Запишем ответ.
Итоги:
На этом уроке мы рассмотрели случаи возможного взаимного расположения сферы и плоскости в пространстве. И выявили, что: если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность; если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку; и если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

 Получите свидетельство
Получите свидетельство Вход
Вход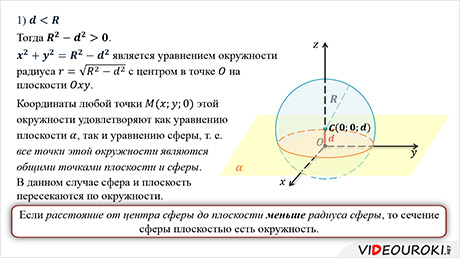



 0
0 17785
17785

