Сфера и шар. Уравнение сферы

На этом уроке мы вспомним понятия сферы и шара. Дадим их определения. Рассмотрим их основные элементы. А также выведем уравнение сферы радиуса  с центром в точке .

Итак, рассмотрим понятия сферы и шара. В окружающем мире предметы имеют очень разнообразные формы. Среди них встречаются так называемые «круглые тела». Особое место среди круглых тел занимает шар.

Итак, шар – это геометрическое тело.

Форму, близкую к форме шара, имеют шарики мороженного, снежный ком, бусинки, светильники.

Некоторые архитектурные сооружения.

Декоративным растениям также придают форму шара.

Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Как окружность, есть граница круга, так и сфера – это граница шара.

Представление о сфере дают полые круглые предметы, например, мячи (футбольный, баскетбольный, волейбольный и т.д.), шарики для украшения ёлки, мыльные пузыри.

А также ставший популярным видом отдыха в наше время «аквазорбинг». Зорб даёт представление о сфере.

Сфера входит в число наиболее привлекательных пространственных фигур. Использование в строительстве и архитектуре конструкций, имеющих форму сферы, придает сооружениям особое величие и служит подтверждением тому, что сфера – достаточно гармоничная геометрическая фигура.

Чтобы уяснить разницу между понятиями шар и сфера, давайте внимательно посмотрим на экран.

Перед вами изображены воздушный шар и бильярдный шар. Отметим, что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.

Определение:

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

А теперь назовём основные элементы сферы.

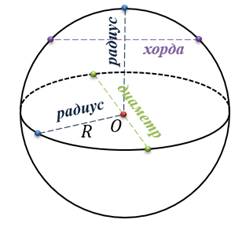
Данная точка называется центром сферы (в нашем случае это точка О), а данное расстояние – радиусом сферы. Радиус сферы часто обозначают латинской буквой .

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Все радиусы одной сферы равны между собой.

Хордой сферы называется отрезок, соединяющий две точки сферы.

Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Любой диаметр сферы равен двум радиусам .

Тело, ограниченное сферой, называется шаром.

Определение:

Шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Центр, радиус, хорда и диаметр сферы называются также центром, радиусом, хордой и диаметром шара.

Т.е. отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара.

Отрезок, соединяющий две точки сферы называется хордой шара.

Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам .

Рассмотрим чертёж.

Перед нами математическое изображение шара. Точка О – это центр шара. Все точки поверхности шара одинаково удалены от центра шара. Понятно, что шар радиуса  с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем  (включая саму точку О), и не содержит других точек.

Хотелось бы обратить внимание на то, что шар может быть получен путём вращения полукруга вокруг его диаметра.

При этом сфера образуется в результате вращения полуокружности вокруг её диаметра.

Задача: отрезок  – хорда сферы, не проходящая через центр сферы . Вычислите расстояние от центра сферы до середины хорды , если радиус сферы равен  см, а длина хорды  равна  см.

Решение: обозначим середину хорды  точкой .

Рассмотрим . Он равнобедренный, т.е. , так как . А как мы знаем, все радиусы одной сферы равны между собой. Отсюда,  (см).

Теперь рассмотрим . Он прямоугольный, так как отрезок  является серединным перпендикуляром проведённым к хорде . Его катет  (см).

Воспользовавшись теоремой Пифагора найдём катет , который как раз таки и есть расстояние от центра сферы до середины хорды . Получаем, что  (см).

Запишем ответ.

Перейдём к уравнению сферы.

Для начала вспомним, что уравнение с тремя переменными , ,  называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности  и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Напомним, что уравнение плоскости, проходящей через точку  и перпендикулярной к ненулевому вектору  имеет следующий вид:

где

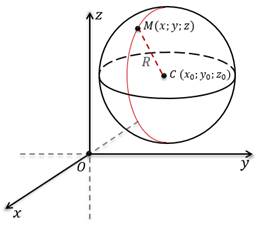
Теперь давайте выведем уравнение сферы радиуса  с центром в точке .

Напомним, что расстояние от произвольной точки  до точки  вычисляется по формуле:

Если точка  лежит на данной сфере, то расстояние , или , т.е. координаты точки  удовлетворяют уравнению:

Если же точка  не лежит на данной сфере, то расстояние , или , т.е. координаты точки  не удовлетворяют уравнению сферы.

Следовательно, в прямоугольной системе координат уравнение сферы радиуса  с центром в точке :

Если уравнение относительно прямоугольных координат  определяет поверхность в пространстве, то ею является сфера.

Задача: напишите уравнение сферы с центром в точке  радиусом равным  см.

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Подставим заданные координаты центра сферы в уравнение. Получим, что уравнение данной нам сферы выглядит так:

Запишем ответ.

Задача: найдите координаты центра и радиус сферы, заданной уравнением: .

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Тогда не трудно заметить, что координаты центра сферы будут равны 2, - 1, 0.

А радиус заданной сферы равен .

Не забудем записать ответ.

Задача: какую поверхность определяет уравнение

 ?

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Преобразуем наше уравнение.

Разделим почленно это уравнение на 4.

Получим, .

Затем выделим полные квадраты. Получим, .  

Преобразуем слагаемые получившегося выражения. Получим, .

Теперь сравним последнее уравнение с уравнением сферы в общем виде. Заметим, что исходное уравнение определяет сферу с центром в точке  и .

Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятия сферы и шара. Узнали, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. А шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Назвали основные элементы сферы и шара. А также вывели уравнение сферы радиуса  с центром в точке .