На этом уроке мы познакомимся с понятием усеченного конуса. Дадим определение усеченного конуса. Назовем и рассмотрим его основные элементы. А затем выведем формулы для вычисления площади боковой поверхности и площади полной поверхности усеченного конуса.
Итак, рассмотрим понятие усечённого конуса.
Вообще вокруг нас существует множество предметов, имеющих форму усечённого конуса. Вафельные стаканчики для мороженного имеют форму усечённого конуса, некоторые стаканы, светильники, ведра обладают формой очень близкой к форме усечённого конуса.

Некоторые архитектурные сооружения также имеют форму усечённого конуса. И многое другое.

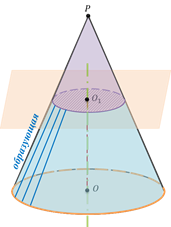
Возьмём произвольный конус и проведём секущую плоскость, параллельную его основанию. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая (нижняя) называется усечённым конусом.
Определение:
Усечённым конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной оси конуса.
Назовём элементы усечённого конуса.
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса.
Высотой усечённого конуса называется отрезок (или его длина), соединяющий центры его оснований.
Прямая  называется его осью.
называется его осью.
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, расположенные между основаниями, называются образующими усечённого конуса.
Все образующие усечённого конуса равны друг другу.
Усечённый конус может быть получен вращением на
 прямоугольной трапеции
вокруг её боковой стороны, перпендикулярной к основаниям.
прямоугольной трапеции
вокруг её боковой стороны, перпендикулярной к основаниям.

На экране вы видите усечённый конус,
полученный вращением прямоугольной трапеции  вокруг стороны
вокруг стороны  , перпендикулярной к
основаниям
, перпендикулярной к
основаниям  и
и  . При этом основания усечённого
конуса образуются вращением оснований
. При этом основания усечённого
конуса образуются вращением оснований  и
и  трапеции, а боковая
поверхность – вращением боковой стороны
трапеции, а боковая
поверхность – вращением боковой стороны  .
.
Выведем формулу для вычисления площади боковой поверхности усечённого конуса.
Для этого нам нужно доказать, что площадь
боковой поверхности усечённого конуса равна  , где
, где  и
и  – радиусы оснований,
– радиусы оснований,  – образующая усечённого
конуса.
– образующая усечённого
конуса.
Доказательство. Пусть  – вершина конуса, из
которого получен усечённый конус,
– вершина конуса, из
которого получен усечённый конус,  – одна из образующих
усечённого конуса, а точки
– одна из образующих
усечённого конуса, а точки  и
и  – центры его оснований.
Причём,
– центры его оснований.
Причём,  . Тогда площадь боковой
поверхности усечённого конуса равна разности боковых поверхностей двух конусов,
т.е.
. Тогда площадь боковой
поверхности усечённого конуса равна разности боковых поверхностей двух конусов,
т.е.  . Преобразуем это
выражение.
. Преобразуем это
выражение.

Заметим, что длина образующей  исходного конуса состоит
из суммы отрезков
исходного конуса состоит
из суммы отрезков  . Используя формулу для
вычисления площади боковой поверхности конуса, получаем:
. Используя формулу для
вычисления площади боковой поверхности конуса, получаем:  .
.
Отсюда, учитывая, что  , получим следующее
выражение
, получим следующее
выражение  .
.
Теперь выразим  через
через  ,
,  и
и  . Прямоугольные
треугольники
. Прямоугольные
треугольники  подобны
по двум углам. Отсюда следует, что
подобны
по двум углам. Отсюда следует, что  , или
, или  .
.
Значит, получаем, что  .
.
Подставим это выражение в формулу.

Упростим.

В итоге приходим к следующей формуле:  .
.
Этим мы с вами вывели формулу для вычисления площади боковой поверхности усеченного конуса.
Таким образом, мы доказали, что площадь
боковой поверхности усечённого конуса равна произведению полусуммы длин
окружностей оснований на длину образующей, где  и
и  – радиусы оснований,
– радиусы оснований,  – образующая усечённого
конуса.
– образующая усечённого
конуса.
Площадью полной поверхности усечённого
конуса называется сумма площадей его боковой поверхности и площади двух
его оснований. Формулу для вычисления площади боковой поверхности усечённого
конуса  мы
с вами вывели выше. Площадь нижнего основания усеченного конуса равна
мы
с вами вывели выше. Площадь нижнего основания усеченного конуса равна  , а площадь меньшего
основания –
, а площадь меньшего
основания –  . Подставим все данные в
формулу.
. Подставим все данные в
формулу.

Отсюда, получаем, что площадь полной
поверхности усеченного конуса можно вычислить по следующей формуле:  .
.
Теперь давайте решим несколько задач.
Задача: длины радиусов оснований
и образующей усечённого конуса равны соответственно  см,
см,  см и
см и  см. Вычислите его высоту.
см. Вычислите его высоту.
Решение: рассмотрим
четырехугольник  .
.

Это есть прямоугольная трапеция с основаниями  и
и  . Высота этой трапеции и
будет высотой нашего усечённого конуса
. Высота этой трапеции и
будет высотой нашего усечённого конуса  . Для того чтобы её
найти, проведём из точки
. Для того чтобы её
найти, проведём из точки  меньшего основания
перпендикуляр на большее основание трапеции
меньшего основания
перпендикуляр на большее основание трапеции  . Фигура
. Фигура  является
прямоугольником, значит противоположные стороны равны, т.е.
является
прямоугольником, значит противоположные стороны равны, т.е.  (см),
(см),  .
.
Рассмотрим  . Он прямоугольный (по
построению). Катет
. Он прямоугольный (по
построению). Катет  (см). Применим теорему
Пифагора и найдём длину катета
(см). Применим теорему
Пифагора и найдём длину катета  . Получаем, что
. Получаем, что  (см). Запишем ответ.
(см). Запишем ответ.
Задача: длины радиусов оснований
усечённого конуса равны  см и
см и  см. Вычислите площадь
боковой поверхности этого конуса, если угол между образующей и плоскостью его
основания равен
см. Вычислите площадь
боковой поверхности этого конуса, если угол между образующей и плоскостью его
основания равен  .
.
Решение: запишем формулу для вычисления площади боковой поверхности усечённого конуса.

Рассмотрим четырёхугольник  .
.

Это есть прямоугольная трапеция с основаниями  и
и  . Высота этой трапеции и
будет высотой нашего усечённого конуса
. Высота этой трапеции и
будет высотой нашего усечённого конуса  .
.
Проведём из точки  меньшего основания
перпендикуляр на большее основание трапеции
меньшего основания
перпендикуляр на большее основание трапеции  . Фигура
. Фигура  является
прямоугольником, значит, противоположные стороны равны, т.е.
является
прямоугольником, значит, противоположные стороны равны, т.е.  (см),
(см),  .
.
Рассмотрим  . Он прямоугольный (по
построению). По условию задачи образующая усечённого конуса наклонена к его
основанию под углом
. Он прямоугольный (по
построению). По условию задачи образующая усечённого конуса наклонена к его
основанию под углом  . Следовательно, катет
. Следовательно, катет  . В свою очередь,
. В свою очередь,  . Применим теорему Пифагора
и найдём длину гипотенузы
. Применим теорему Пифагора
и найдём длину гипотенузы  треугольника
треугольника  . Получаем, что
. Получаем, что  (см). Значит, образующая
нашего усечённого конуса равна
(см). Значит, образующая
нашего усечённого конуса равна  (см).
(см).
Подставим длины радиусов и образующей усечённого
конуса в формулу для вычисления площади боковой поверхности. Посчитаем.
Получим, что площадь боковой поверхности усеченного конуса равна  (см2).
(см2).
Не забудем записать ответ.
Итоги:
На этом уроке мы познакомились с понятием усечённого конуса. Узнали, что усечённым конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной оси конуса. Назвали основные элементы усечённого конуса. А также вывели формулы для вычисления площади боковой поверхности и площади полной поверхности усечённого конуса.

 Получите свидетельство
Получите свидетельство Вход
Вход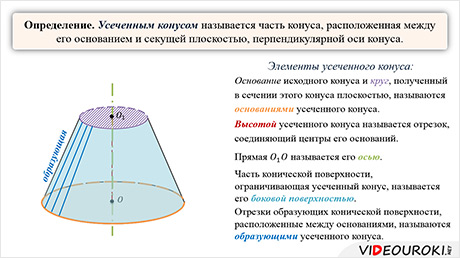



 0
0 14307
14307