На этом уроке мы выведем и научимся применять формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса.
Для начала давайте вспомним, что же это за геометрическое тело – конус.

Итак, тело, ограниченное
конической поверхностью и кругом с границей  , называется конусом.
, называется конусом.
Напомним, что боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.

На экране изображён конус, у которого радиус
равен  , а
образующая равна
, а
образующая равна  . Боковую
поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на
плоскость, разрезав её по одной из образующих.
. Боковую
поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на
плоскость, разрезав её по одной из образующих.
Давайте представим, что боковую поверхность
конуса разрезали по образующей  и развернули
таким образом, что получился круговой сектор
и развернули
таким образом, что получился круговой сектор  .
.

Стороны  и
и  которого
являются двумя краями разреза боковой поверхности конуса.
которого
являются двумя краями разреза боковой поверхности конуса.
Развёрткой боковой поверхности
конуса является круговой сектор. Обратите внимание, радиус сектора равен
образующей конуса, т.е.  .
А длина дуги сектора равна длине окружности основания конуса, т.е. равна
.
А длина дуги сектора равна длине окружности основания конуса, т.е. равна  .
.
За площадь боковой поверхности конуса
принимается площадь её развёртки. Выразим площадь боковой поверхности конуса
через его образующую  и радиус
основания
и радиус
основания  .
.
Площадь кругового сектора – развёртки боковой
поверхности конуса – равна  , где
, где  – градусная
мера дуги
– градусная
мера дуги  .
.
Выразим  через длину
дуги и радиус окружности. Длина дуги окружности с градусной мерой
через длину
дуги и радиус окружности. Длина дуги окружности с градусной мерой  и радиусом
и радиусом  равна
равна  . С другой
стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто
восемьдесят равно
. С другой
стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто
восемьдесят равно  . Отсюда,
. Отсюда,  . Подставим
это выражение в формулу площади боковой поверхности конуса. Тогда площадь
боковой поверхности конуса равна
. Подставим
это выражение в формулу площади боковой поверхности конуса. Тогда площадь
боковой поверхности конуса равна  . Т.е.
площадь боковой поверхности конуса с образующей
. Т.е.
площадь боковой поверхности конуса с образующей  и радиусом
основания
и радиусом
основания  выражается следующей
формулой:
выражается следующей
формулой:  .
.
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Теперь выведем формулу для вычисления площади полной поверхности конуса.
Вообще, площадью полной поверхности
конуса называется сумма площадей боковой поверхности и основания. Формулу
для вычисления площади боковой поверхности конуса  мы с вами выразили выше, а площадь круга равна
мы с вами выразили выше, а площадь круга равна  . Подставим
все данные в формулу.
. Подставим
все данные в формулу.

Упростим. Отсюда, получаем, что площадь полной
поверхности конуса равна  .
.
А сейчас давайте решим несколько задач на применение выведенных формул.
Задача: образующая  конуса равна
конуса равна
 см, а его
высота –
см, а его
высота –  см.
Вычислите площадь боковой поверхности конуса.
см.
Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для вычисления площади боковой поверхности конуса.

Теперь внимательно рассмотрим рисунок.

Напомним, что высота конуса перпендикулярна
его основанию. А, значит, она перпендикулярна любой прямой, лежащей в плоскости
основания конуса. Следовательно, высота конуса  .
.
Рассмотрим  . Он
прямоугольный. Применяя теорему Пифагора, найдём длину стороны
. Он
прямоугольный. Применяя теорему Пифагора, найдём длину стороны  , которая и
является радиусом основания конуса. Получаем, что ОА равно
, которая и
является радиусом основания конуса. Получаем, что ОА равно 
 .
.
Подставим длину образующей конуса и его радиус
в формулу для вычисления площади боковой поверхности конуса. Посчитаем.
Получим, что площадь боковой поверхности конуса равна  .
.
Запишем ответ.
Задача: радиус основания конуса
равен  дм, а
площадь его осевого сечения –
дм, а
площадь его осевого сечения –  дм2.
Вычислите площадь боковой поверхности конуса.
дм2.
Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для вычисления площади боковой поверхности конуса.

Теперь рассмотрим рисунок.

Напомним, что осевым сечением конуса называется сечение
конуса плоскостью, проходящей через его ось, и представляет собой равнобедренный треугольник, основание которого –
диаметр основания конуса, а боковые стороны – образующие конуса. Значит,  – равнобедренный.
– равнобедренный.
Так как по
условию задачи радиус основания конуса равен 9 дм, то основание осевого сечения
равно 
 .
.
Напомним, что
площадь треугольника равна половине произведения длины основания на высоту  . Выразим из формулы высоту
. Выразим из формулы высоту  . Получаем, что высота треугольника, а она является и
высотой конуса, равна
. Получаем, что высота треугольника, а она является и
высотой конуса, равна 
 .
.
Рассмотрим  . Он прямоугольный, так как
. Он прямоугольный, так как  . Применяя теорему Пифагора, найдём длину
. Применяя теорему Пифагора, найдём длину  . Получаем, что
. Получаем, что 
 . Обратите внимание, гипотенуза
. Обратите внимание, гипотенуза  есть образующая нашего конуса.
есть образующая нашего конуса.
Подставим
найденную длину образующей конуса и его радиус в формулу для вычисления площади
боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности
конуса равна 
 .
.
Не забудем записать ответ.
Задача: прямоугольный треугольник, длины катетов которого
равны  см и
см и  см, вращается вокруг меньшего катета. Вычислите
площадь полной поверхности конуса, образованного при этом вращении.
см, вращается вокруг меньшего катета. Вычислите
площадь полной поверхности конуса, образованного при этом вращении.
Решение: запишем формулу для вычисления площади полной поверхности конуса.

Рассмотрим  . Он прямоугольный по условию.
. Он прямоугольный по условию.

Воспользуемся теоремой
Пифагора и найдём длину гипотенузы  , которая и является образующей конуса. Имеем,
, которая и является образующей конуса. Имеем,  .
.
Так как по
условию задачи треугольник вращается вокруг меньшего катета, то радиус
основания конуса, образованного при этом вращении, равен  .
.
Подставим длину
образующей конуса и его радиус в формулу для вычисления площади полной
поверхности конуса. Посчитаем. Получим, что площадь полной поверхности нашего
конуса равна  .
.
Запишем ответ.
Итоги:
На этом уроке мы вывели формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса. А также научились их применять при решении задач.

 Получите свидетельство
Получите свидетельство Вход
Вход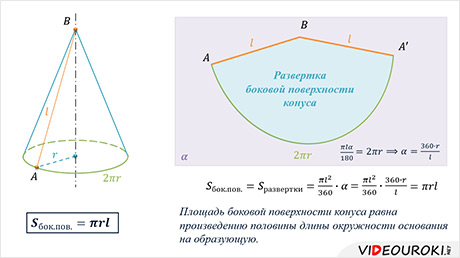



 0
0 15625
15625

