Ранее с вами научились преобразовывать рациональные выражения. Тождественные преобразования, которые умеем выполнять: это приведение подобных слагаемых; раскрытие скобок; разложение на множители; приведение рациональных дробей к общему знаменателю. Также для преобразования рациональных выражений используют формулы сокращённого умножения.

Теперь же мы ввели новую операцию – операцию извлечения квадратного корня. Вы уже знаете, что арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Давайте рассмотрим примеры преобразований выражений, которые содержат квадратные корни.
Задание: упростите выражение.
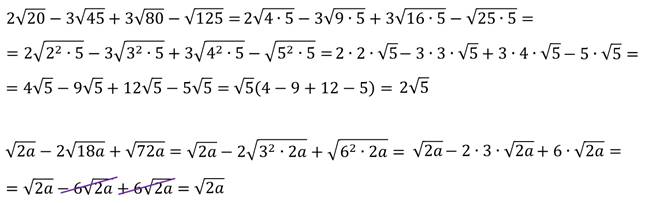
Задание: преобразуйте выражения.
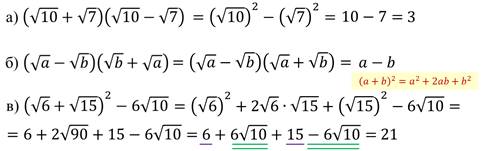
Задание: сократите дробь.
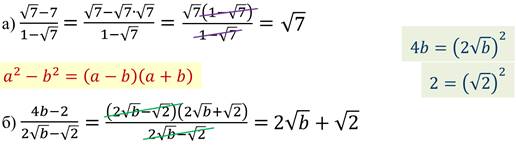
Очень важное место в преобразовании выражений, содержащих квадратные корни, занимает избавление от иррациональности в знаменателе или числителе дроби. Можно рассмотреть это на простом примере.
Например: преобразуем дробь так, чтобы знаменатель не содержал квадратного корня.
Как сделать так, чтобы знаменатель дроби не содержал квадратный корень? Следует вспомнить основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то значение дроби не изменится
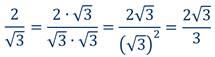
Обратите внимание, дробь 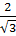 мы
заменили тождественно равной ей дробью
мы
заменили тождественно равной ей дробью 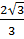 .
Причем, в знаменателе второй дроби нет знака корня. В таких случаях говорят,
что мы освободились от иррациональности в знаменателе дроби.
.
Причем, в знаменателе второй дроби нет знака корня. В таких случаях говорят,
что мы освободились от иррациональности в знаменателе дроби.
Задание: освободиться от иррациональности в знаменателе дроби.


 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 42532
42532

