Получите свидетельство
Вход
«Превратить магнетизм в электричество…»
Майкл Фарадей
Данная тема будет посвящена рассмотрению основных формул и методических рекомендаций по решению задач на электромагнитную индукцию
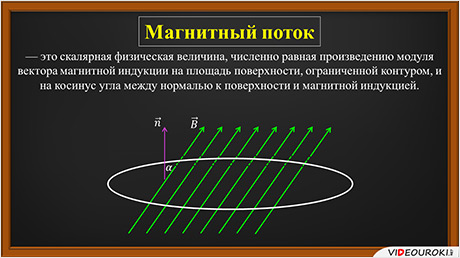
Рассмотрим основные понятия электромагнитной индукции. Магнитный поток – это скалярная физическая величина, численно равная произведению модуля вектора магнитной индукции на площадь поверхности, ограниченной контуром, и на косинус угла между нормалью к поверхности и направлением линий магнитной индукцией.
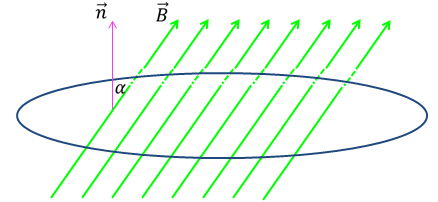
Изменение магнитного потока влечет за собой такое явление, как электромагнитная индукция. Чем быстрее изменяется магнитный поток, тем большая сила тока возникает в замкнутом контуре.
В результате явления электромагнитной индукции, в контуре возникает электродвижущая сила – она так и называется ЭДС индукции.
Поскольку сила тока связана с индукцией порождаемого им магнитного поля, а магнитная индукция, в свою очередь, связана с магнитным потоком, возникает явление самоиндукции. Самоиндукция – это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. То есть, при изменении силы тока, в цепи возникает индукционный ток, который стремится препятствовать этому изменению. В связи с этим, вводится такая величина, как индуктивность – коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. Иными словами, индуктивность характеризует способность проводника влиять на быстроту установления тока в цепи. Она, конечно, обнаруживает себя только при изменении силы тока в цепи.
Сведём в таблицу основные формулы по рассматриваемой теме.
|
Формула |
Описание формулы |
|
|
Магнитный поток через контур площадью S, где B – модуль вектора магнитной индукции, a – угол между направлением вектора магнитной индукции и нормалью к плоскости контура. |
|
|
ЭДС индукции, возникающая в контуре при изменении магнитного потока на величину DF за промежуток времени Dt. |
|
|
ЭДС
индукции, возникающая в движущемся со скоростью |
|
|
Коэффициент самоиндукции (индуктивность) контура. |
|
|
ЭДС самоиндукции, возникающая в контуре при изменении силы тока на величину DI за промежуток времени Dt. |
|
|
Индуктивность
соленоида объёмом V,
где m – магнитная проницаемость среды,
m0
– магнитная постоянная |
|
|
Энергия магнитного поля катушки с индуктивностью L, где I – сила тока, F – магнитный поток. |
|
|
Энергия магнитного поля соленоида объёмом V, где B — модуль вектора магнитной индукции. |
проводнике
длиной 
,
где a – угол между направлением
вектора магнитной индукции и направлением вектора скорости.
Гн/м,
n – число
витков на единицу длины.
Методические рекомендации по решению задач на электромагнитную индукцию
1. Установить причину изменения магнитного потока через контур. Исходя из формулы, причиной может стать либо изменение магнитной индукции поля, либо изменение площади контура, а также угла между направлением линий магнитной индукции и нормалью к плоскости контура (чаще всего, это поворот рамки с током).
2. Записать закон электромагнитной индукции (закон Фарадея).
3. Если речь идет о поступательном движении проводника, применить формулу, по которой вычисляется ЭДС индукции в движущемся проводнике.
4. Определить изменение магнитного потока, рассматривая его в выбранные моменты времени t1 и t2 (как правило, это должны быть те моменты времени, которые описываются в задаче).
5. Подставить найденное выражение для изменения магнитного потока в закон Фарадея. При необходимости, используя дополнительные уравнения, составить систему и решить её относительно искомых величин.
0
4066
