Логарифмическая функция, её свойства и график

Вы уже знаете, что выражение  определено при , , .

Пусть задано основание логарифма , . Тогда каждому   соответствует  . Тем самым задана функция .

Запомните! Функцию , где  — заданное число,  и , называют логарифмической.

Давайте перечислим основные свойства логарифмической функции.

Итак, логарифмическая функция обладает следующими свойствами:

1.  Область определения логарифмической функции — множество всех положительных чисел.

Это следует из определения логарифма, так как выражение  имеет смысл только при .

2.  Множество значений логарифмической функции — множество  всех действительных чисел.

Докажем это свойство. Пусть задано , которое принадлежит . Тогда функция  принимает значение  при , так как  . Таким образом, любое действительное число  принадлежит множеству значений логарифмической функции. Что и требовалось доказать.

3.  Логарифмическая функция не является ограниченной.

Это следует из того что множество значений логарифмической функции – множество всех действительных чисел.

4.  Логарифмическая функция является возрастающей на промежутке , то есть на всей области определения, если , и убывающей, если

.

Докажем это свойство. Пусть , ,  – произвольные положительные числа. Докажем, что если  , то , то есть .

По основному логарифмическому тождеству  и  можно записать так: , .

Так как по условию    , то  .

Из этого неравенства по свойству степени с основанием  следует, что  .

Случай 2. Пусть , ,  – произвольные положительные числа.

Докажем, что если , то  .

По основному логарифмическому тождеству  и  можно записать так: , .

Так как по условию  , то  

Из этого неравенства при  следует, .

Что и требовалось доказать.

Хотелось бы отметить, что справедливыми будут и обратные утверждения:

если  и , где , , то ;

если  и , где , , то .

5.  Если , то функция  принимает положительные значения при , отрицательные при .

Если , то функция  принимает положительные значения при , отрицательные при  .

Докажем это свойство.

Функция принимает значение, равное 0, при  и является возрастающей на промежутке , если , и убывающей, если  .

Что и требовалось доказать.

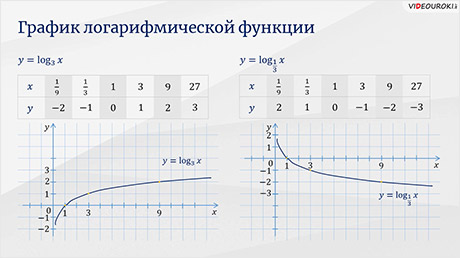
Как же будет выглядеть график такой функции?

Итак, давайте построим графики функций  (здесь ) и   (здесь ).

Для этого, как обычно, найдём сначала координаты некоторых точек графика и заполним таблицу значений функций.

Отметим эти точки на координатной плоскости и соединим их.

Получившиеся кривые являются графиками функций   и  .

Заметим, что значение равное 0 логарифмическая функция принимает в точке 1. Это следует из того, что  при любом , так как  .

Ось О  является вертикальной асимптотой графика функции  .

При решении уравнений часто используется следующая теорема: если , где , , , , то .

Доказательство. Предположим, что  , например  .

Если , то из неравенства  следует, что ;

если , то из неравенства  следует, что .

В обоих случаях получилось противоречие с условием . Следовательно, .

Что и требовалось доказать.

Логарифмическая функция  и показательная функция , где  и  взаимно обратны.

Докажем это. Решим уравнение  .

Получим .

Поменяем местами  и .

Получим .

Что и требовалось доказать.

Так как функции  и  взаимно обратны, то свойства любой из них можно установить, зная свойства другой.

Например, множеством значений функции  является множество , поэтому областью определения функции  является множество . Функция  возрастает, если , поэтому функция   также возрастает, если .

А теперь давайте приступим к практической части нашего урока.

Задание. Найдите область определения функции .

Решение.

Ответ: .