Вопросы занятия:
• вывести формулы для нахождения производных произвольных показательных и логарифмических функций.
Материал урока
На прошлых уроках мы рассмотрели, чему равна производная частного случая показательной функции:

Теперь давайте попробуем найти, чему равна производная функции y = ax.

Рассмотрим пример.

Рассмотрим еще один пример.

Изучая натуральный логарифм, мы говорили, что:

Попробуем теперь вывести формулу для нахождения производной произвольной логарифмической функции.
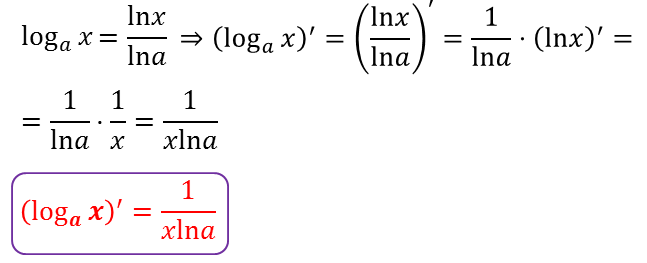
Рассмотрим пример.

Рассмотрим еще один пример.
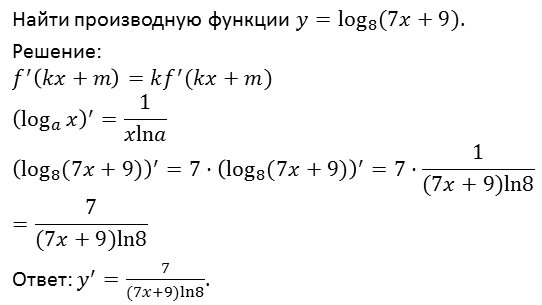
Давайте еще раз запишем формулы нахождения производных показательных и логарифмических функций:
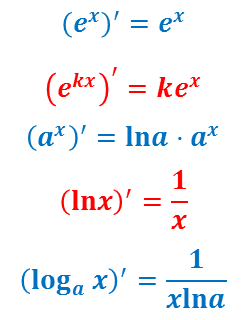

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 6251
6251

