Натуральный логарифм. Функция y=ln x ее свойства, график, дифф.

Вопросы занятия:

• рассмотреть натуральный логарифм как логарифм с основанием е;

• рассмотреть функцию y = ln x, её свойства, график и производную.

Материал урока

Когда мы вводили понятие логарифма, мы упоминали про натуральный логарифм, мы говорили, что натуральным называется логарифм по основанию е.

Но тогда мы еще не знали, что это за число.

Теперь же мы можем рассмотреть натуральные логарифмы подробно.

Напомним, что е – это основание показательной функции y = a^x, касательная

к графику которой в точке с абсциссой 0 пересекает ось Ox под углом в 45°.

Давайте еще раз повторим определение натурального логарифма. Логарифм, основанием которого является число е называется натуральным.

Для натуральных логарифмов было введено специальное обозначение.

То есть:

График логарифмической функции симметричен графику показательной функции с таким же основанием относительно прямой y = x.

То есть:

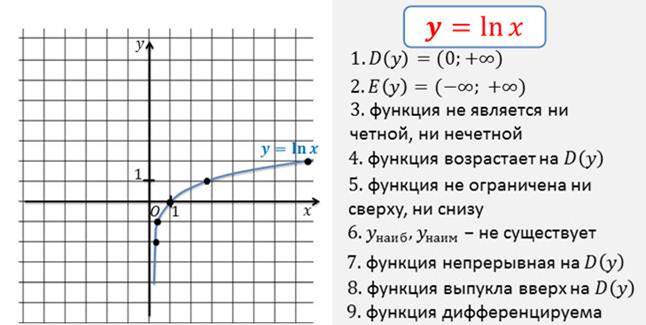
График этой функции будет отличаться от графиков других логарифмических функции тем, что угол между касательной к графику в точке с абсциссой 1 и осью Ox равен 45°.

По графику легко записать основные свойства функции:

Производная:

Покажем геометрическое обоснование этой формулы.

Мы получили общее правило вычисления производной обратной функции: производная обратной функции есть величина, обратная производной данной функции.

Строго доказательства этого утверждения мы рассматривать не будем.

Кратко это правило можно записать так:

Если y = ln x, то получим:

Рассмотрим несколько примеров.

Пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

Давайте еще раз повторим основные свойства функции y = ln x.