Число е. Функция y=e^x ее свойства, график, дифф.

Вопросы занятия:

• рассмотреть число е как основание показательной функции;

• рассмотреть функцию y = e^x, её свойства, график и производную.

Материал урока

Прежде чем перейти к изучению нового материала, давайте вспомним основные свойства и график показательной функции.

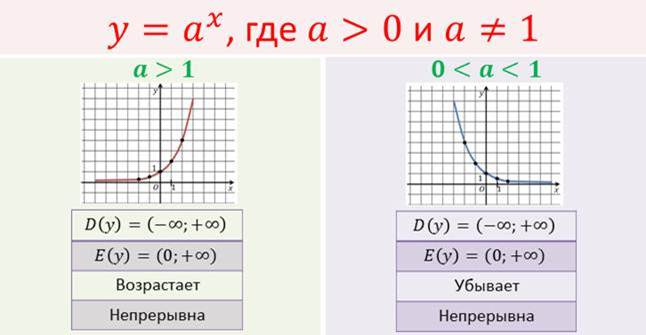
Давайте рассмотрим график функции:

Проведем касательную к точке x = 0.

Если строить точно, а затем измерить угол между касательной и положительным направлением оси Ox, то можно убедиться в том, что:

Теперь давайте построим график функции:

Проведем касательную к точке x = 0.

Если измерить этот угол, то получится:

Если же мы построим график функции:

Проведем касательную к точке x = 0.

Измерим получившийся угол, то получим:

То есть:

То есть, логично предположить, что есть такое основание а, для которого соответствующий угол между касательной к точке x = 0 и осью абсцисс равен 45°.

Очевидно, что это основание заключено в промежутке от 2 до 3.

 Было доказано, что такое число существует, его принято обозначать буквой е. Установлено, что число е – иррациональное, то есть представляет собой бесконечную десятичную непериодическую дробь:

На практике обычно полагают:

Существует множество способов запоминания несколько первых знаков после запятой числа е.

Изобразим график этой функции:

Ее отличие от остальных экспонент будет только в том, что угол между касательной к графику в точке x = 0 и осью абсцисс равен 45°.

По графику легко записать основные свойства функции игрек равно е в степени икс.

Без доказательства примем, что:

Рассмотрим несколько примеров.

Пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

Давайте еще раз повторим основные свойства функции: