Переход к новому основанию логарифма

Вопросы занятия:

• ввести формулу перехода к новому основанию логарифма;

• познакомить со свойствами логарифмов, которые следуют из этой формулы.

Материал урока

Прежде чем перейти к изучению нового материала, давайте повторим некоторый теоретический материал.

Решая логарифмические уравнения и неравенства у нас встречались логарифмы, основания которых либо были одинаковыми, либо приводились к одинаковым путем простейших преобразований. А как же быть, если в уравнении или неравенстве присутствуют логарифмы, основания которых нельзя путем простейших преобразований привести к одинаковому числу?

Например, можно ли как-нибудь преобразовать:

и

И если да, то какое основание будет у такого логарифма и какой будет подлогарифмическая функция?

Для решения такого рода заданий используется следующая теорема:

Теорема:

Эта формула называется формулой перехода к новому основанию логарифма.

Докажем эту формулу.

Теперь можно очень просто логарифм по основанию 2 преобразовать в логарифм с основанием 3.

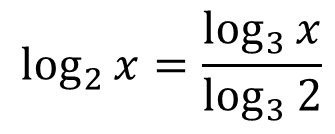
То есть:

Таким образом, мы получили, что:

То есть логарифмы одной функции, но разных оснований отличаются в k раз.

Аналогично, можно записать, что:

Это равенство выполняется для логарифмов по произвольному основанию.

Рассмотрим частные случаи данной формулы.

Следствие 1.

Например:

Доказательство.

Следствие 2.

Например:

Доказательство.

Рассмотрим пример.

Рассмотрим еще один пример.

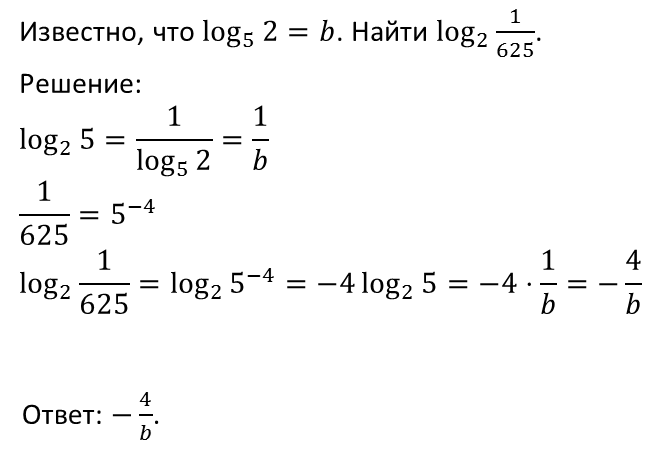
Рассмотрим еще один пример.

Рассмотрим еще один пример.

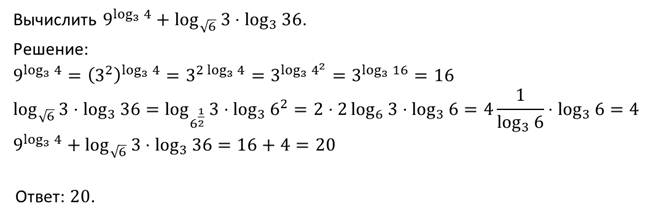
Давайте еще раз повторим формулы, с которыми мы познакомились на этом уроке: