Первообразная

Вопросы занятия:

• ввести понятие первообразной;

• рассмотреть свойства первообразных.

Материал урока

Давайте вернемся к теме производная и вспомним физический и геометрический смысл производной. Напомним, что физический смысл производной состоит в следующем:

Геометрический смысл производной состоит в следующем:

Мы знаем, что производная применяется и для исследования функций и для решения задач на оптимизацию.

Наряду с прямой задачей нахождения мгновенной скорости по закону прямолинейного движения тела, логично было бы рассмотреть и обратную задачу, то есть можно ли определить закон движения тела, если известна мгновенная скорость в определенный момент времени?

Рассмотрим одну физическую задачу.

И пусть скорость движения ежика в момент времени t задается формулой v = g(t). Найти закон движения ежика. В данном случае ежика будем рассматривать как материальную точку.

Решение.

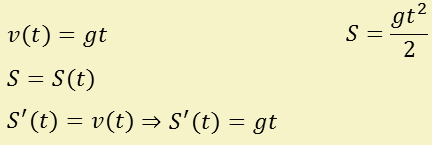
Но это решение не совсем верное. На самом деле эта задача будет иметь бесконечно много решений: ее решением будет любая из функций вида:

Чтобы задача имела единственное решение, уточним условие.

Укажем координату ежика в какой-нибудь момент времени, например при t = 0. То есть:

Тогда:

В алгебре взаимно обратным операциям присваивают разные названия, специальные обозначения, например: возведение в степень и извлечение корня, косинус, арккосинус и так далее. Мы знаем, что процесс нахождения производной называется дифференцированием. Для операции, обратной дифференцированию введено название – интегрирование.

Сформулируем определение.

Как правило, промежуток икс большое не указывают, но подразумевают.

Например:

Зная формулы для нахождения производных, нетрудно составить таблицу для нахождения первообразной.

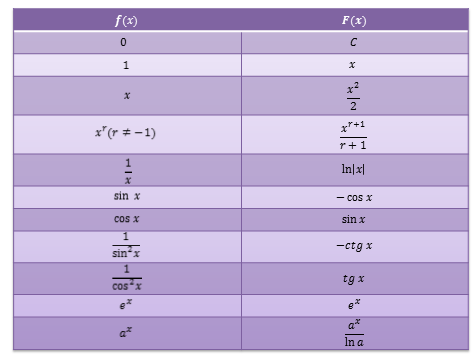
Давайте рассмотрим отдельно первообразную для функции:

Понятно, что в таблице записана одна из первообразных каждой функции, потому что, для того, чтобы записать все первообразные, необходимо к каждой функции добавить слагаемое C, где C – это произвольное действительное число.

Для нахождения первообразных, как и производных, используют не только формулы, указанные в таблице, но и некоторые правила. Они очень тесно связаны с правилами вычисления производных.

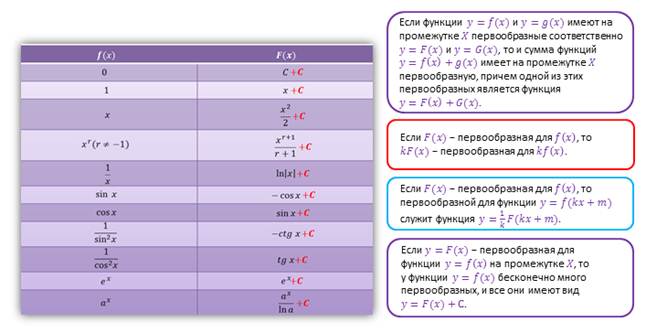
Итак, правилу о вычислении производной суммы двух функций можно поставить в соответствие правило о нахождении первообразной суммы двух функций.

Другими словами, первообразная суммы равна сумме первообразных.

Рассмотрим пример.

Правилу о вынесении постоянного множителя за знак производной, соответствует аналогичное правило первообразных.

Рассмотрим пример.

Мы помним, что производная произведения двух функций не равна произведению производных соответствующих функций и производная частного не равна частному производных. Поэтому нет и правил для нахождения первообразных произведения и частного функций.

Теорема 1.

Доказательство.

Рассмотрим пример.

Рассмотрим еще одну теорему.

Теорема 2.

Эту теорему доказывают в курсе высшей математики.

Давайте теперь в каждом из рассмотренных примеров запишем все первообразные для исходных функций:

Теперь давайте еще раз повторим таблицу первообразных основных функций, и основные правила нахождения первообразных: