В формулировке любой теоремы можно выделить две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – это то, что надо доказать.
Например, рассмотрим один из признаков параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Здесь условие утверждения: если при пересечении двух прямых секущей накрест лежащие углы равны. А заключение: прямые параллельны.
Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением - условие данной теоремы.
Теорема:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Доказательство:
Пусть прямые а и b параллельны и пересечены секущей CD. Доказать, что накрест лежащие углы 1 и 2 равны.
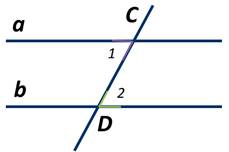
Предположим, что углы 1 и 2 не равны. Тогда от луча CD отложим ∠ЕCD=∠2 так, чтобы ∠ЕCD и ∠2 были накрест лежащими углами при пересечении прямых СЕ и b секущей CD.
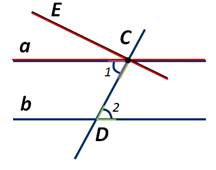
По построению эти накрест лежащие углы равны, а поэтому прямая CE параллельна прямой b. Получили, что через точку С проходят две прямые (а и CЕ) параллельные прямой b. А это противоречит аксиоме параллельности прямых. Следовательно, предположение неверно и угол ∠1=∠2. Что и требовалось доказать.
Пример.
Прямая АВ параллельна прямой CD, АD - биссектриса угла BAC, а ∠ADC=50 градусов. Чему равна градусная мера ∠CAD?
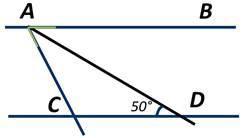
Так как прямые АВ и CD параллельны и AD - секущая при этих параллельных прямых, то накрест лежащие углы ADC и BAD равны. Значит, ∠BAD=50 градусов.
Так как AD - биссектриса ∠BAC, то ∠CAD=∠BAD. Следовательно, градусная мера ∠CAD=50 градусов.
Пример.
Прямые АВ и CD параллельны. Отрезок АВ=СD. Доказать, что прямая АС параллельна прямой BD.
Рассмотрим треугольник ABD и треугольник ACD.
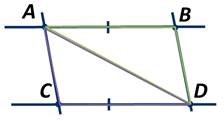
АВ=CD по условию задачи, AD - общая. А углы BAD и ADC равны как накрест лежащие углы при параллельных прямых АВ и CD и секущей АD. Следовательно, треугольники ABD и ACD равны по первому признаку равенства треугольников. А значит, у них соответственные стороны и углы равны.
То есть ∠CAD=∠BDA. А эти углы являются накрест лежащими при прямых AC и BD и секущей AD. Это означает, что прямые AC и BD параллельны. Что и требовалось доказать.
Пример.
На рисунке ∠CBD=∠ADB. Доказать, что ∠ВСА=∠CAD.
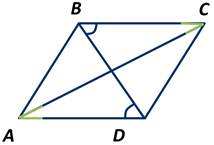
Углы CBD и ADB - накрест лежащие углы при прямых AD и BC и секущей BD. А так как эти углы равны, то прямые AD и BC параллельны.
∠ВСА и ∠CAD являются накрест лежащими при параллельных прямых AD и BC и секущей АС, а следовательно, они равны. Что и требовалось доказать.
Отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
Например, если углы вертикальные, то они равны. А вот если углы равны, то это ещё не означает, что они вертикальные.


 Получите свидетельство
Получите свидетельство Вход
Вход



 3
3 29245
29245


Здравствуйте.
Спасибо за ценное замечание. Ошибка, на которую Вы указали, исправлена. Ознакомиться с исправленным текстом урока Вы можете на этой же странице.
Здравствуйте. Ваш запрос принят в работу службой технической поддержки сайта. Пожалуйста, ожидайте ответ.
Я конечно извиняюсь, НО вы бы хоть сами почитали, что вы пишите ! У Вас тут как минимум ошибка в доказательстве и в первом же примере ! Проверяйте !