На предыдущих уроках мы рассмотрели ряд теорем, доказательства которых опираются на уже доказанные ранее теоремы. В таком случае возникает вопрос: А на чём основаны доказательства самых первых теорем? Ответ такой: Доказательства самых первых теорем основаны на аксиомах.
Определение:
Аксиома (в переводе с греческого «аксиос» означает ценный, достойный) - это утверждение, устанавливающее некоторое свойство и принимаемое без доказательства.
Аксиомы возникли из опыта, они являются наглядно очевидными и не вызывают сомнений.
Нам уже известны некоторые аксиомы. Например:
1. Через любые две точки проходит прямая и притом только одна.

2. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

3. От любого луча в заданную сторону можно отложить угол, равный данному неразвёрнутому углу, и притом только один.

Аксиома:
Пусть дана прямая а и не лежащая на ней произвольная точка О. Докажем, что через точку О можно провести прямую, параллельную прямой а.

Проведём две прямые: сначала прямую c, перпендикулярно к прямой а, а затем прямую b, перпендикулярно к прямой c.

Получили, что прямые а и b перпендикулярны к прямой c, а значит, они параллельны.
А теперь возникает вопрос: можно ли провести ещё одну прямую через точку О, параллельную прямой а? Ответ на этот вопрос не является очевидным. Оказывается, что утверждение о единственности прямой, проходящей через данную точку и параллельной прямой, не может быть доказано на основании остальных аксиом и само является аксиомой.
Аксиома параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы:
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

2. Если две прямые параллельны третьей, то они параллельны.

Пример.
Дан треугольник АВС. Сколько прямых, параллельных стороне АС можно провести через вершину В?

Так как по аксиоме параллельных прямых через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной:

То есть через точку В можно провести единственную прямую, параллельную стороне АС треугольника АВС.
Геометрия, которую вы изучаете в школе, называется «евклидовой геометрией», так как её основы заложил древнегреческий математик Евклид. Его подход к построению геометрии основан на том, что сначала формулируются аксиомы, а затем путём рассуждений доказываются другие утверждения.
В 18-м веке русский математик Николай Лобачевский создал другую геометрию. Лобачевский считал аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жёсткое.
И он предположил, что через точку, не лежащую на данной прямой, проходит более чем одна прямая, параллельная данной. В результате получилась новая система определений и теорем. Эту геометрию назвали геометрией Лобачевского.
Как оказалось, геометрия Лобачевского точнее описывает геометрию Вселенной, чем геометрия Евклида. Результатами геометрии Лобачевского пользовался учёный Альберт Энштейн.

 Получите свидетельство
Получите свидетельство Вход
Вход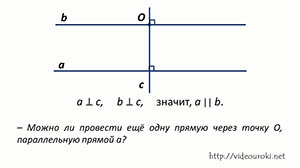



 0
0 20314
20314

