Признак параллельности прямых по сумме градусных мер односторонних углов

Первый признак параллельности прямых:

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Второй признак параллельности прямых:

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема:

Если при пересечении двух прямых секущей сумма градусных мер односторонних углов равна 180 градусам, то прямые параллельны.

Доказательство:

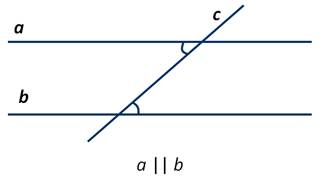
Пусть при пересечении прямых а и b секущей c сумма односторонних углов 1 и 2 равна 180 градусам.

Так как углы 2 и 3 являются смежными, то ∠2+∠3=180 градусов.

Из равенств ∠1+∠2=180 градусов и ∠2+∠3=180 градусов следует, что ∠1=∠3. А поскольку ∠1 и ∠3 являются накрест лежащими, то прямые а и b параллельны. Теорема доказана.

Пример.

При пресечении двух параллельных прямых а и b секущей c образовано 8 углов. ∠1=130 градусов. Найдите остальные углы.

Так как прямая а параллельна прямой b, то ∠7=∠1=130 градусов как внешние накрест лежащие углы.

∠5=∠1=130 градусов как соответственные углы.

∠3=∠1=130 градусов как вертикальные.

По свойству смежных углов ∠2=180-∠1=50 градусов.

∠8=∠2=50 градусов как внешние накрест лежащие углы.

∠6=∠2=50 градусов как соответственные углы.

∠4=∠2=50 градусов как вертикальные углы.

Пример.

В треугольнике АВС стороны АВ и ВС равны. А ∠ВАС=60 градусов. Луч СD - биссектриса угла ВСЕ смежного с углом АСВ. Доказать, что прямая АВ параллельна прямой СD.

Так как АВ=ВС, то треугольник АВС является равнобедренным. Углы ВАС и АСВ равны как углы при основании равнобедренного треугольника и равны 60 градусов.

Углы ВСЕ и АСВ являются смежными, поэтому ∠ВСЕ=180-∠АСВ=120 градусов.

∠BCD=60 градусов, так как по условию задачи СD - биссектриса угла ВСЕ.

Тогда ∠ВАС + ∠DСА=180 градусов.

Следовательно, прямые АВ и СD параллельны. Что и требовалось доказать.

Пример.

В треугольнике АВС, ∠А=40 градусов, а ∠В=70 градусов. Через вершину В проведена прямая ВD так, что луч ВС является биссектрисой угла АВD. Доказать, что прямые ВD и АС параллельны.

Рассмотрим прямые АС, ВD и секущую прямую АВ. Углы ВАС и АВD - внутренние односторонние.

По условию задачи ВС - биссектриса угла АВD, а значит ∠АВС=∠СВD=70 градусов. Тогда угол ∠АВD=140 градусов.

Угол ∠ВАС+∠АВD=40+140=180 градусов. А так как эти углы являются внутренними односторонними, то получаем, что прямая АС параллельна прямой BD. Что и требовалось доказать.