Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов

Вспомним теорему о равенстве накрест лежащих углов:

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

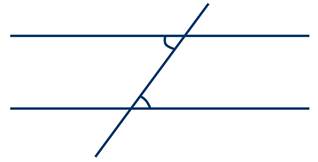
Теорема:

Если две параллельные прямые пересечены секущей, то соответственные углы равны.

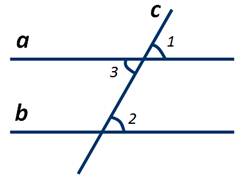
Доказательство:

Пусть параллельные прямые а и b пересечены секущей c. Необходимо доказать, что соответственные углы 1 и 2 равны. Так как прямая а параллельна прямой b, то накрест лежащие углы 2 и 3 равны. ∠1 и ∠3 равны как вертикальные. Из равенств ∠2=∠3 и ∠1=∠3 следует, что ∠1=∠2. Теорема доказана.

Пример.

Пусть прямая MN параллельная биссектрисе AD треугольника АВС.

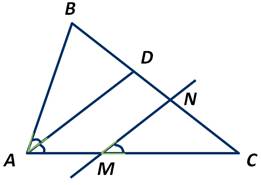
Тогда ∠NMC=∠BAD. Действительно, углы NMC и DAC равны как соответственные углы, а ∠DAC=∠BAD, так как AD - биссектриса.

Теорема:

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.

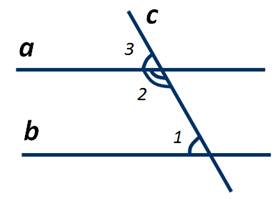
Доказательство:

Пусть параллельные прямые а и b пересечены секущей c. Доказать, ∠1+∠2=180 градусов. Так как прямая а параллельна прямой b, то соответственные ∠1 и ∠3 равны. ∠2+∠3=180 градусов, так как углы 2 и 3 смежные. Тогда, из равенств угол ∠1=∠3 и ∠2+∠3=180 градусов, следует, что ∠1+∠2=180 градусов. Теорема доказана.

Например: пусть прямая DE параллельна стороне АВ треугольника АВС. Тогда ∠BAD+∠ADE=180 градусов.

Пример.

Луч BD - биссектриса угла АВС, прямая DE параллельна прямой АВ, а ∠ЕDB=32 градуса. Чему равен ∠CED?

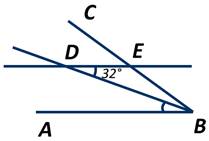
Углы BDE и ABD равны как внутренние накрест лежащие углы при параллельных прямых АВ и DE и секущей BD. То есть ∠ABD=32 градуса. Тогда ∠АВС=64 градуса, так как ВD - его биссектриса.

Углы АВС и CED являются соответственными углами при параллельных прямых АВ и DE и секущей ВС, а значит, они равны. Следовательно, ∠CED=64 градуса.

Пример.

Градусная мера одного из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, меньше градусной меры другого на 26 градусов. Вычислить градусные меры этих углов.

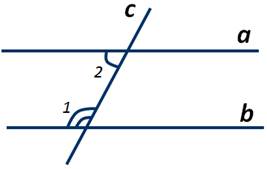
Пусть а и b параллельные прямые, прямая c - секущая при этих параллельных прямых, а ∠1 и ∠2 - внутренние односторонние.

Пусть ∠1=x, тогда ∠2=x-26. Так как ∠1 и ∠2 являются внутренними односторонними при параллельных прямых а и b и секущей с, то их сумма равна 180 градусов, то есть ∠1+∠2=180 градусов.

Тогда:

Получаем: