Блез Паскаль, великий французский учёный 17-го века, заметил, что у всех треугольников сумма 3-х углов равна 180 градусов. И у него возник вопрос: «Как это доказать?»
И он отрезал ножницами два уголка треугольника и приложил их к третьему углу. В результате получился развёрнутый угол, градусная мера которого, как вам уже известно, равна 180 градусов.

Теорема:
Сумма углов треугольника равна 180 градусов.
Доказательство:
Пусть АВС - произвольный треугольник. Доказать, что ∠А+∠В+∠С= 180 градусов.
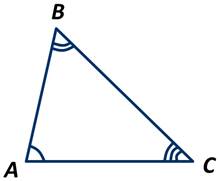
Проведём прямую а через точку В параллельно стороне АС.
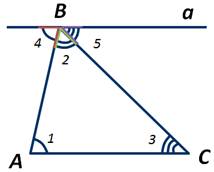
∠1 и ∠4 - внутренние накрест лежащие углы при параллельных прямых а и АС и секущей АВ. А значит, ∠1=∠4. ∠3 и ∠5 являются внутренними накрест лежащими при параллельных прямых а и АС и секущей ВС. Следовательно, ∠3=∠5.
Сумма градусных мер ∠4, ∠2 и ∠5 равна градусной мере развёрнутого угла с вершиной в точке В, то есть ∠4+∠2+∠5=180 градусов.
А так как ∠1=∠4, ∠3=∠5, то получаем, что ∠1+∠2+∠3=180 градусов. То есть ∠А+∠В+∠С=180 градусов. Теорема доказана.
Из теоремы следует:
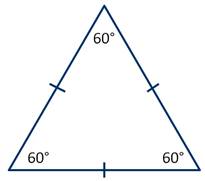
1. Углы равностороннего треугольника равны по 60 градусов.
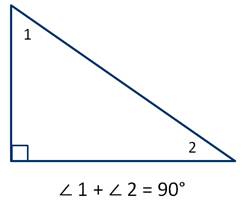
2. Сумма острых углов прямоугольного треугольника равна 90 градусов.
Определение:
Внешним углом треугольника называют угол, смежный с каким-либо углом треугольника.
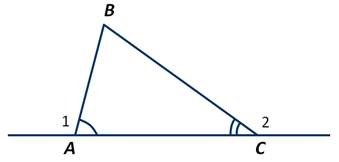
Например, ∠1 - внешний угол треугольника АВС, смежный с ∠ВАС. ∠2 - внешний угол, смежный с ∠АСВ.
Теорема:
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Доказательство:
Пусть АВС - произвольный треугольник. Доказать, что градусная мера ∠4 равна сумме градусных мер углов 1 и 2, не смежных с ним.
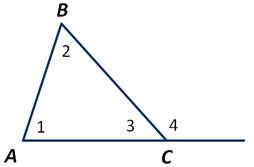
Сумма градусных углов 3 и 4 равна градусной мере развёрнутого угла, то есть ∠3+∠4=180 градусов. А по теореме о сумме градусных мер углов треугольника ∠1+∠2+∠3=180 градусов. Из полученных двух равенств следует, что ∠1+∠2=∠4. Что и требовалось доказать.
Пример.
Стороны АВ и ВС треугольника АВС равны. ∠А=42 градуса. Чему равна градусная мера угла В?
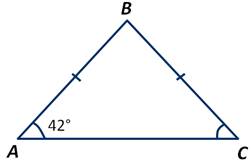
Так как АВ=ВС, то треугольник АВС является равнобедренным. Нам известно, что углы при основании равнобедренного треугольника равны. А значит, ∠С=42 градуса.
По теореме о сумме углов треугольника ∠А+∠В+∠С=180 градусов. Из этого равенства получаем:
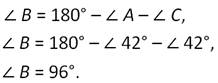
Пример.
На рисунке ∠ВСD=110 градусов, а ∠ВАС=45 градусов. Найти градусную меру ∠АВЕ.
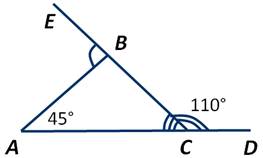
Так как углы ВСD и ВСА - смежные, то:
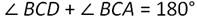
Тогда:
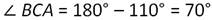
Искомый ∠АВЕ является внешним углом нашего треугольника, смежным с ∠АВС. А значит:
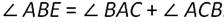
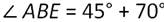
Пример.
В равнобедренном треугольнике АВС с основанием АС отрезок ВD является высотой. Найдите градусные меры углов треугольника ABD, если ∠АВС=56 градусов.
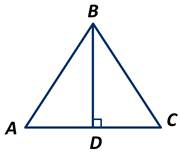
Так как треугольник АВС - равнобедренный, то высота ВD, проведённая к основанию, является также и биссектрисой. Значит:
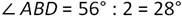
∠АDВ=90 градусов, так как ВD - высота.
По теореме о сумме углов треугольника, получаем:




 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 16061
16061

