Получите свидетельство
Вход
На этом уроке мы познакомимся с действием возведение в степень. Узнаем, что означают выражения «квадрат» и «куб» числа.
Мы с вами уже знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче – в виде произведения.
Пример
Произведение, в котором все множители равны друг другу, тоже можно записать короче.
Пример
Здесь число 6 показывает количество одинаковых множителей.
Вообще, произведение n равных друг другу множителей, обозначается
Где а – любое натуральное число.
Читают это произведение: «а в степени n»,
либо «а в n–ой степени»,
т.е. 
равно
произведению числа а самого на себя n раз.
Определение
В данной записи число а называют основанием степени, число n –
показателем степени, а само выражение – называют
степенью.
Пример
Читают «четыре в пятой степени равно одной тысячи двадцати четырём». Здесь 4 – основание степени, 5 – показатель степени и число 1024 – пятая степень числа 4.
Здесь «восемь во второй степени равно шестьдесят четыре».
Вторую степень часто называют иначе. Произведение 8 ∙ 8 называют квадратом числа 8 и записывают:
В буквенной записи пишут так:
Посмотрите внимательно на экран. Здесь вы видите таблицу квадратов первых 10–ти натуральных чисел:
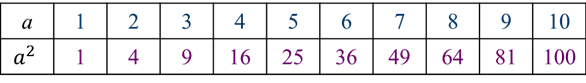
В её правильности можно легко убедиться, зная таблицу умножения. Возьмём для проверки несколько чисел, например 3, 5 и 7.
Следующее произведение:
Здесь «два в третьей степени равно 8».
Третья степень числа также имеет и иное название. Произведение 2 ∙ 2 ∙ 2 называют кубом числа 2 и обозначают
В буквенном виде можно записать так:
Где а – любое натуральное число.
Посмотрите на экран. Вы видите таблицу кубов первых 10–ти натуральных чисел:
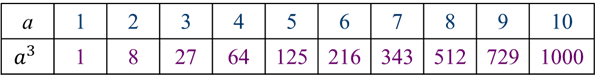
Первую степень числа считают равной самому числу.
Пример
Показатель 1–ой степени обычно не пишут.
Мы с вами уже знаем, что
Запомните ещё одно правило для определения порядка выполнения действий при вычислении значения числового выражения:
Если выражение содержит действия разных ступеней, то сначала выполняют действия в скобках, потом – действия третьей ступени, после них – действия второй ступени и, наконец, - действия первой ступени.
Пример
Найдём значение выражения:
Итоги
Итак, сегодня на уроке мы с вами научились возводить число в степень, а также узнали, что называют квадратом и кубом числа.
0
3157
