Решение систем уравнений второй степени

Способы решения систем уравнений второй степени:

·        графический;

·        подстановки;

·        алгебраического сложения;

·        введения новой переменной.

Пример.

Решим систему уравнений способом подстановки:

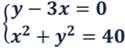
Выполним преобразования:

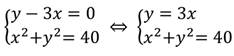
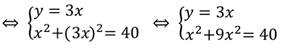
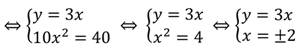
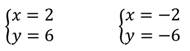
Данная система уравнений имеет два решения: (2; 6) и (-2; -6).

Алгоритм способа подстановки:

·        выразить из уравнения первой степени одну переменную через другую.

·        подставить полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной.

·        решить получившееся уравнение с одной переменной.

·        найти соответствующие значения второй переменной.

Пример.

Решить систему способом алгебраического сложения:

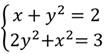
Суть метода: нужно сделать так, чтобы в уравнениях при одной и той же переменной множители являлись противоположными числами.

В данном случае:

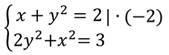
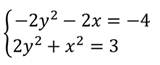
Выполним покомпонентное сложение двух уравнений:

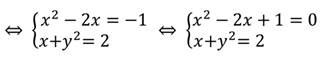
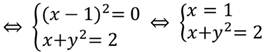
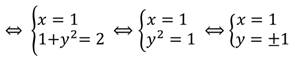
Данная система уравнений имеет два решения: (1; 1) и (1; -1).

Пример.

Решить систему уравнений способом введения новой переменной:

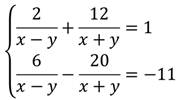
Введем переменную:

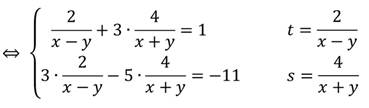
Решим данную систему:

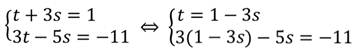
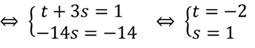
Теперь выполним обратную подстановку:

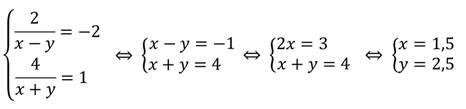
Решением данной системы является пара (1,5; 2,5).