Вопросы занятия:
· Исследование методов решения уравнений, которые нельзя решить традиционно, путём построения компьютерных моделей.
Моделирование любых процессов начинается с записи формальной модели на языке определённой области знаний: математики, физики, химии, биологии, экономики.
В алгебре формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.
Точные решения существуют только для некоторых уравнений определённого вида (линейные, квадратные, тригонометрические и другие), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные).
Например, нельзя точно найти корни уравнения x2 = 8 – х путём равносильных алгебраических преобразований. Но такое уравнение можно решать приближённо графическими и численными методами.

Такие уравнения проще и точнее можно решить путём построения интерактивных компьютерных моделей.
Итак, рассмотрим графический способ решения уравнений.
Нужно найти корни уравнения x2 = 8 – х.
Построение графиков функций может использоваться для грубо приближенного решения уравнений. Для уравнений вида f(x) = g(x), где f(x) и g(x)— это некоторые непрерывные функции. Абсциссы точек пересечения этих графиков и будут корнями данного уравнения. Корень определяется «на глаз», то есть приближённо.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций. При использовании электронных таблиц, Microsoft Excel, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью, например, если использовать метод Подбор параметра.

Решим уравнение x2 = 8 – х средствами Microsoft Excel.
Запускаем Microsoft Excel;
Для построения графика функции нам необходима таблица значений.
В ячейку А1 вводим текст «х», в ячейку A2 — f(x), а ячейку А3 – g(x).
В ячейку В1 вводим число (-5), в ячейку С1 – число (-4,8);
выделим диапазон ячеек (В1;С1), подведём указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму чёрного крестика, протянуть маркер выделения вправо до значения 5.
В ячейку В2 вводим формулу: =В1^2 и скопируем содержимое ячейки Бэдва в диапазон ячеек (C2; AZ2). Вся строка выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
В ячейку B3 вводим формулу: =8-B1 и скопируем содержимое ячейки B2 в диапазон ячеек (C3; AZ3).
Мы построили таблицу значений, теперь построим графики функций. Для этого выделяем диапазон ячеек (A1; AZ2). Теперь на вкладке Вставка, в разделе диаграммы нажимаем на значок раскрывающегося списка Вставить точечную диаграмму. В раскрывшемся меню выбираем Точечная.
Итак, мы построили график функции f(x) = x2. Теперь на вкладка Работа с диаграммами выбираем вкладку Конструктор. В разделе Данные нажимаем Выбрать данные.
В окошке элементы легенды (ряды) нажимаем добавить. В раскрывшемся окне Изменение ряда выбираем Имя ряда – g(x), значения x – указываем диапазон ячеек (B1; AZ1). Значения y указываем диапазон ячеек (A3; AZ3).

Мы построили графики функций f(x) = x2 и g(x)=8-x.
Решениями уравнения x2=8-x будут абсциссы точек пересечения этих графиков.
Выделим первую точку пересечения и поднесём к ней указатель мыши, появится окошко комментария, в котором будет указана координата данной точки. Итак, первым корнем нашего уравнения будет (-3,4). Аналогично найдём второй корень. Второй корень нашего уравнения число 2,4.
Как мы уже говорили Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть «хорошими».
Возможности электронных таблиц позволяют находить приближенные значения корней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения x точек пересечения графика функции y(x) с осью абсцисс.
Найдём приближённое решение уравнения с заданной точностью методом Подбор параметра.
Начнём с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен -3,4. В таблице значений функции этот аргумент размещается в ячейке J1.
Выделяем ячейку J4 и переходим на вкладку Данные. В разделе Работа с данными нажимаем Анализ «что-если». В раскрывшемся меню выбираем Подбор параметра.
В открывшемся диалоговом окне Подбор параметра в поле Значение ввести требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке J1.
Нажимаем Ок.
В окне Результат подбора мы увидим информацию о величине подбираемого и подобранного значения функции:
В ячейке Джей один выводится подобранное значение аргумента (-3,37225) с требуемой точностью (0,0001).
Установить точность можно путём установки в ячейках таблицы точности представления чисел. Для этого нужно в меню Формат ячеек выбрать Число, а затем Числовой. Теперь установить требуемую точность.
Аналогично найдём приближенное значение второго корня уравнения с заданной точностью.
Итак, по графику определяем, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 2,4. В таблице значений функции этот аргумент размещается в ячейке AM1.
Выделяем ячейку AM4 и переходим на вкладку Данные. В разделе Работа с данными нажимаем Анализ «что-если». В раскрывшемся меню выбираем Подбор параметра.
В открывшемся диалоговом окне Подбор параметра в поле Значение ввести требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке AM1.
Нажимаем Ок.
В окне Результат подбора мы увидим информацию о величине подбираемого и подобранного значения функции:
В ячейке AM1 выводится подобранное значение аргумента (2,37229) с требуемой точностью (0,0001).
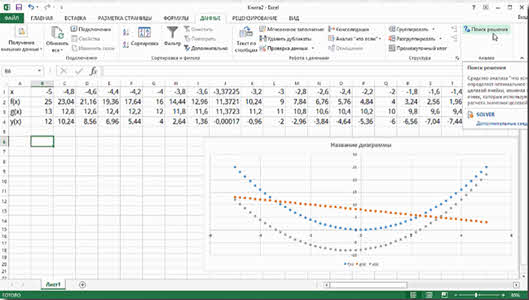
Рассмотрим ещё один способ решения уравнений средствами Excel
Часто при решении практических задач возникают ситуации, когда в Вашем распоряжении есть математическая модель исследуемого процесса, например, закон ценообразования, но Вы не знаете, при каком значении входящего в неё параметра можно достичь поставленной цели.
Решение таких задач можно искать методом перебора. Однако в лучшем случае на это уходит много времени.
В Excel такие способы решения реализованы как поиск значения аргумента, удовлетворяющего конкретному значению функции.
Найдём корни нашего уравнения x2 = 8 – х с помощью средства анализа Поиск решения. А затем сравним полученные результаты.
Итак, нам необходимо вызвать программу Поиск решения и сообщить ей, где расположены данные. Для этого необходимо сначала загрузить её.
Откроим вкладку Файл и выберем пункт Параметры.
Далее выбираем команду Надстройки, а затем в окне Управление выбираем пункт Надстройки Excel. Нажимаем кнопку Перейти.
Теперь в окне Доступные надстройки установим флажок Поиск решения и нажимаем кнопку ОК.
После загрузки надстройки "Поиск решения" на вкладки Данные в группе Анализ становится доступна команда Поиск решения. Выбираем её, после чего перед нами открывается соответствующая форма.
Далее необходимо выполнить следующий алгоритм:
в ячейку A1 введём x, в ячейку B1 - значение, например, -5. В ячейку А2 введём y(x). В ячейку B2 необходимо ввести значение вспомогательной функции, то есть = x2 -8 + х.
Теперь устанавливаем курсор в ячейку B2 и на вкладке Данные в группе Анализ нажимаем Поиск решения.
Введём координату ячейки с целевой функцией. В нашем случае это B2. (Заметим, что если перед этим установить курсор на ячейку B2, как мы и сделали, то ввод произойдёт автоматически).
Поставить отметку «До значения» и указываем 0.
В поле «Изменяя ячейки переменных» введём B1, то есть сообщить, какое место отведено под значения корня нашей функции.
В поле «В соответствии с ограничениями» ничего вводить не нужно. В поле «Выберите метод решения» выбираем Поиск решения нелинейных задач метолом ОПГ.
Теперь нажимаем «Найти решение». В результате в ячейке B1 отображается корень нашего уравнения. x приблизительно равно 2,37228.
Теперь хотелось бы получить второй корень. В задаваемом нами интервале видно, что график дважды пересекает ось Оx, следовательно, нужно найти ещё один корень. Однако, сколько бы мы не вызывали окно подбора параметра, компьютер с упорством, достойным лучшего применения, продолжает выдавать первый корень.
При поиске решения находится только оптимальное решение.
Также, обратите внимание, что во всех 3 вариантах решения, мы получили приблизительно равные корни нашего уравнения. Следовательно, можно сделать вывод, что уравнение мы решили правильно.

Теперь давайте попробуем решить другое уравнение на основе уже созданной модели.
Итак, решим уравнение х2-1=sinx.
Для построения графика функции нам необходима таблица значений. Она у нас уже есть, нам нужно только изменить значения в соответствующих ячейках. В ячейке B2 необходимо дописать (-1), и скопировать содержимое ячейки в диапазон (B2; AZ2). Теперь исправим значение в ячейке B3: запишем =sinB1, нажимаем Enter затем скопируем в диапазон (B3;AZ3).
Обратите внимание, графики функций автоматически изменились, и мы видим, что они пересекаются в двух точках. То есть, по графику мы на глаз можем определить, что приблизительно, корнями данного уравнения являются числа (-0,6) и (1,4).

Найдём более точные значения корней.
С помощью инструмента Поиск решения найдём более точное приближенное значение первого корня. Для этого в ячейку B7 запишем целевую функцию: = B6 ^2-1-sinB6. Ставим курсор в ячейку B6 и на вкладке Данные нажимаем Поиск решения. Заполним таблицу, итак, целевая функция у нас уже указана. Дальше ставим =0, затем указываем ячейку, в которую будет записано значение переменной. Нажимаем найти решение.
Получили значение одного корня. Он приблизительно равен (-0,63673).
Более точное приблизительное значение второго корня найдём методом Подбор параметра.
Итак, значения вспомогательной функции y(x) у нас уже посчитались. Находим по таблице значение, при котором знак вспомогательной функции меняется, это значение 1,4.
Выделяем ячейку AG4 и переходим на вкладку Данные. В разделе Работа с данными нажимаем Анализ «что-если». В раскрывшемся меню выбираем Подбор параметра.
В открывшемся диалоговом окне Подбор параметра в поле Значение вводим требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке AG1.
Нажимаем Ок. В результате мы получили более точное приближенное значение второго корня: 1,4096.

 Получите свидетельство
Получите свидетельство Вход
Вход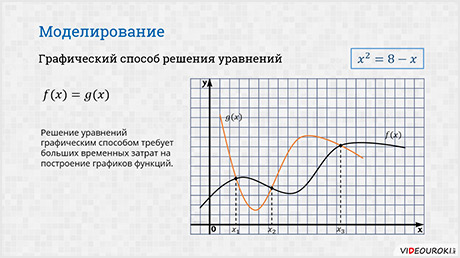



 0
0 4283
4283

