Взаимно обратные числа

Сегодня на уроке мы познакомимся с новым для вас понятием «взаимно обратные числа» и научимся определять обратные числа данным.

Давайте умножим дробь 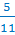 на дробь .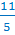

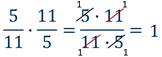
После сокращения мы получим .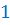

Говорят, что число 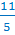  обратно числу  .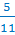

Произведение 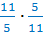  также равно единице.

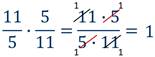
Поэтому число 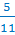  обратно числу  .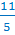

Числа 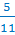  и 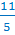 взаимно обратны.

Задание

Найдём произведение чисел 8 и  , 1 и .

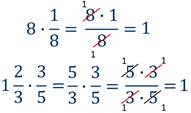
Числа 8 и  , 1 и  также взаимно обратны.

Что общего вы заметили в этих примерах, кроме того, что пары этих чисел называют взаимно обратными. Правильно! Произведение этих чисел равно 1.

Определение

Два числа, произведение которых равно единице, называют взаимно обратными.

С помощью букв взаимно обратные числа можно записать так:

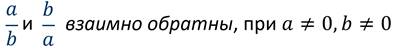
И это можно проверить:

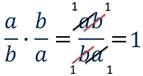
Если одно из двух взаимно обратных чисел – правильная дробь, то другое обязательно неправильная дробь.

Число 1 взаимно обратно самому себе, а число 0 не имеет обратного себе числа.

Значит, чтобы выяснить, являются ли два числа взаимно обратными, их надо перемножить.

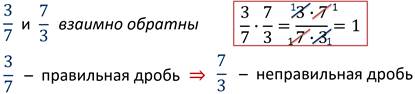
Если ответ равен единице, то числа – взаимно обратные.

Запомним несколько полезных правил:

Чтобы найти число взаимно обратное данному, надо:

1)    Если число натуральное нужно представить его в виде дроби и перевернуть (поменять местами числитель и знаменатель).

2)    Если число обыкновенная дробь нужно дробь перевернуть, а затем выделить целую часть.

3)    Если число смешанное нужно представить его в виде неправильной дроби, затем перевернуть.

4)    Если число десятичная дробь нужно представить его в виде дроби, затем перевернуть и выделить целую часть.

Задание

Найдите обратное число данному.

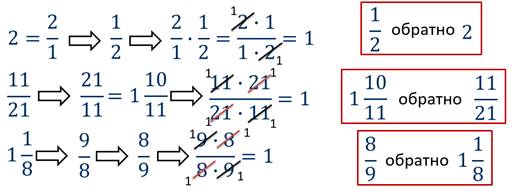
Задание

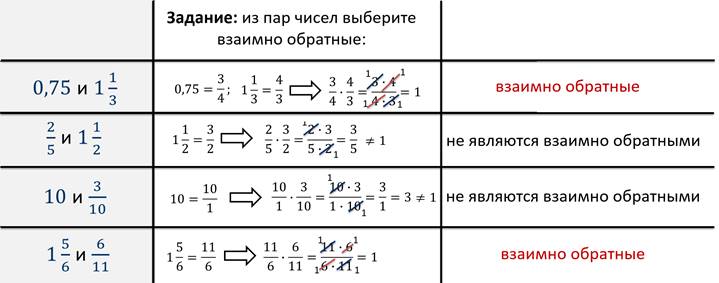
Из пар чисел представленных на экране выберите взаимно обратные:

Итоги

Итак, сегодня на уроке мы познакомились с взаимно обратными числами и научились находить обратное число данному.