Напомним, что любое конечное множество уравнений называется системой уравнений.
Систему уравнений принято записывать с помощью фигурной скобки.
Общий вид системы двух уравнений с двумя переменными:
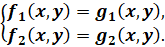
Решением
системы двух уравнений с двумя переменными называется пара
чисел 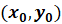 ,
при подстановке которых вместо соответствующих переменных
,
при подстановке которых вместо соответствующих переменных 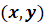 оба
уравнения системы обращаются в верные числовые равенства.
оба
уравнения системы обращаются в верные числовые равенства.
Решить систему уравнений – значит найти все её решения или доказать, что решений нет.
Две системы уравнений называются равносильными, если они имеют одно и то же множество решений. Если обе системы не имеют решений, то они также считаются равносильными.
Теоремы о равносильности систем уравнений.
1. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе уравнение заменить равносильным, то полученная система будет равносильна заданной.
2. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе заменить суммой или разностью обоих уравнений системы, то полученная система будет равносильна заданной.
3.
Если обе части уравнения 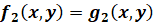 ни
при каких
ни
при каких 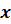 ,
,
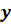 одновременно
не обращаются в нуль, то следующие системы равносильны:
одновременно
не обращаются в нуль, то следующие системы равносильны:
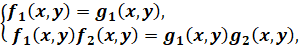
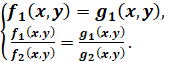
Вспомним основные методы решения систем уравнений. Итак, основными методами решения систем уравнений являются метод алгебраического сложения, метод подстановки и метод введения новых переменных.
Метод алгебраического сложения. Сущность этого метода заключается в следующем:
1. обе части первого уравнения умножают на некоторый множитель, обе части второго уравнения умножают на другой множитель (если это требуется). Эти множители подбираются так, чтобы коэффициенты при одной из переменных в обоих уравнениях стали противоположными числами;
2. уравнения почленно складывают и решают полученное уравнение с одной переменной;
3. вторую переменную находят подстановкой найденного значения первой переменной в одно из уравнений системы.
Решите
систему уравнений 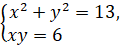 .
.
Решение.
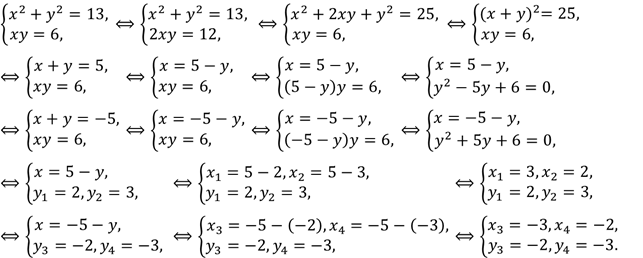
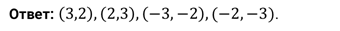
Решите
систему уравнений 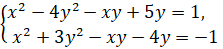 .
.
Решение.
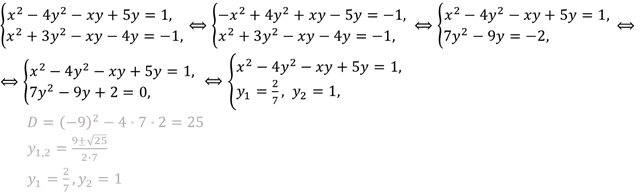
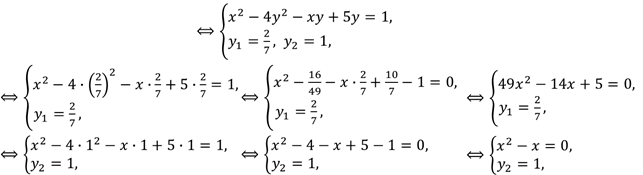
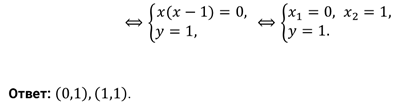
Метод подстановки. Сущность этого метода заключается в следующем:
1) выражают из какого-либо уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующие значения второй переменной.
Решите
систему уравнений 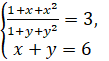 .
.
Решение.
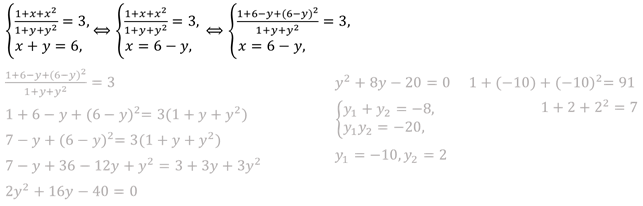
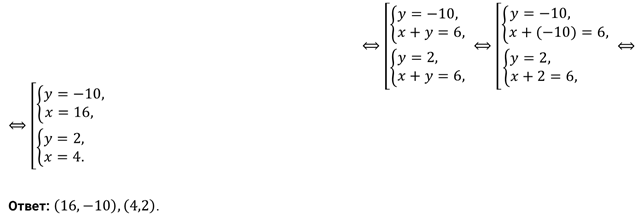
Решите
систему уравнений 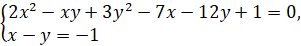 .
.
Решение.
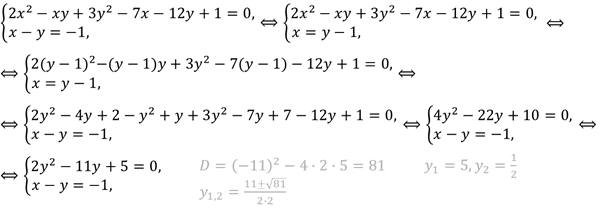
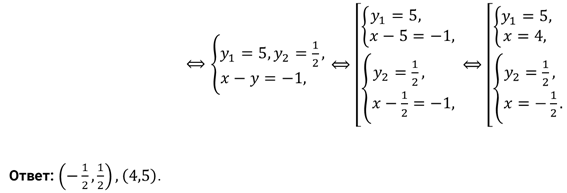
Метод введения новых переменных. При сопутствующем выборе вспомогательных переменных иногда решение исходной системы можно свести к решению более простой системы уравнений, чем исходная.
Решите
систему уравнений  .
.
Решение.


Решите
систему уравнений  .
.
Решение.



Рассмотренные методы решения систем уравнений применяются и к решению систем, содержащих показательную и логарифмическую функции.
Решите
систему уравнений 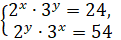 .
.
Решение.
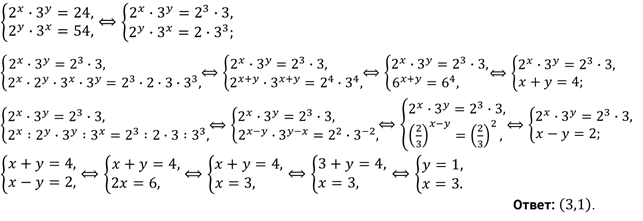
Решите
систему уравнений  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход





 2834
2834